(本小题满分12分)设a∈R,函数f (x) =
 ,其中e是自然对数的底数.
,其中e是自然对数的底数.
(Ⅰ)求函数f (x)的单调区间;
(Ⅱ)当– 1 < a < 0时,求f (x)在[1,2]上的最小值.
已知A、B、C是直线l上的三点,向量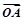 、
、 、
、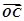 满足
满足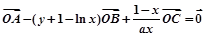 ,(O不在直线l上
,(O不在直线l上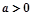 )
)
(1)求 的表达式;
的表达式;
(2)若函数 在
在 上为增函数,求a的范围;
上为增函数,求a的范围;
(3)当 时,求证:
时,求证: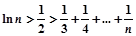 对
对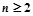 的正整数n成立.
的正整数n成立.
设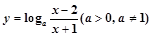 的定义域为
的定义域为 ,值域为
,值域为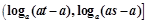 ,
,
(1)求证: ;
;
(2)求a的取值范围.
某公司生产一种产品的固定成本是10000元,每生产一件产品需要另外投入80元,又知市场对这种产品的年需求量为800件,且销售收入函数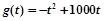 ,其中t是产品售出的数量,且
,其中t是产品售出的数量,且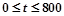 (利润=销售收入
(利润=销售收入 成本).
成本).
(1)若x为年产量,y表示利润,求 的解析式;
的解析式;
(2)当年产量为多少时,求工厂年利润的最大值?
已知向量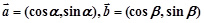 且
且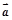 与
与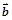 满足关系式:
满足关系式: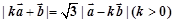 .
.
(1)用k表示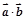 ;
;
(2)证明: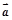 与
与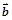 不垂直;
不垂直;
(3)当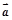 与
与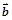 的夹角为
的夹角为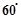 时,求k的值.
时,求k的值.
设有两个命题:
命题p:不等式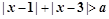 对一切实数x都成立;
对一切实数x都成立;
命题q:已知函数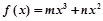 的图象在点
的图象在点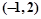 处的切线恰好与直线
处的切线恰好与直线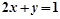 平行,且
平行,且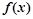 在
在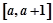 上单调递减.
上单调递减.
若命题p或q为真,求实数a的取值范围.