某公司生产一种产品的固定成本是10000元，每生产一件产品需要另外投入80元，又知市场对这种产品的年需求量为800件，且销售收入函数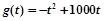
，其中t是产品售出的数量，且
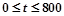（利润=销售收入
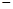成本）.
（1）若x为年产量，y表示利润，求
的解析式；
（2）当年产量为多少时，求工厂年利润的最大值？
（（本小题满分12分）
已知
,
,若
是
的必要不充分条件，求实数m的取值范围.
（本小题满分12分）
若一动点F到两定点
、
的距离之和为4.
（Ⅰ）求动点F的轨迹方程；
（Ⅱ）设动点F的轨迹为曲线C，在曲线C任取一点P，过点P作
轴的垂线段PD，D为垂足，当P在曲线C上运动时，线段PD的中点M的轨迹是什么？
（本小题满分11分）
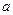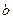从含有两件正品
,
和一件次品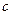
的3件产品中每次任取一件，连续取两次，每次取出后放回，求取出的两件产品中恰有一件是次品的概率．
（示范高中）如图，已知椭圆
（a＞b＞0）的离心率
，过点
和
的直线与原点的距离为
．
(1)求椭圆的方程;
（2）已知定点
，若直线
与椭圆交于
、
两点．问：是否存在
的值，使以
为直径的圆过
点?请说明理由．
(本小题满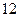分
分)
（普通高中）已知椭圆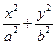
（a＞b＞0）的离心率
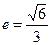，焦距是函数
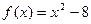的零点.
（1）求椭圆的方程；
（2）若直线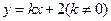
与椭圆交于
、
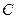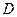两点,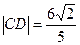
，求k的值．