已知曲线
,点
是曲线
上的点
.
(1)试写出曲线
在点
处的切线
的方程,并求出
与
轴的交点
的坐标;
(2)若原点
到
的距离与线段
的长度之比取得最大值,试求试点
;
(3)设
与
为两个给定的不同的正整数,
与
是满足(2)中条件的点
的坐标,证明:
在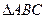 中,角
中,角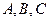 所对的边分别为
所对的边分别为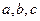 ,已知
,已知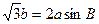 ,
,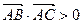 ,
,
(1)求角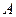 ;
;
(2)若 ,
,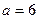 ,求
,求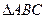 的面积。
的面积。
已知函数 在区间
在区间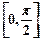 上的最大值为2
上的最大值为2 .
.
(1)求常数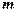 的值;
的值;
(2)在 中的角
中的角 ,
,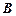 ,
, 所对的边是
所对的边是 ,
, ,
, ,若
,若
 ,
, 面积为
面积为 .求边长
.求边长 .
.
三棱柱 的直观图和三视图如下图所示,其侧视图为正三角形(单位cm)
的直观图和三视图如下图所示,其侧视图为正三角形(单位cm)
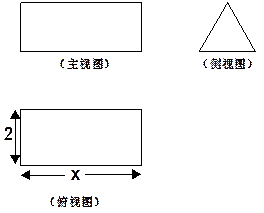
⑴当x=4时,求几何体的侧面积和体积
⑵当x取何值时,直线AB1与平面BB1C1C和平面A1B1C1所成角大小相等。
如图,已知四棱锥P﹣ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC=3,侧面PBC⊥底面ABCD,O是BC的中点.
(1)求证:DC∥平面PAB;
(2)求四棱锥P﹣ABCD的体积.
已知数列 的前
的前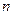 项和
项和 满足:
满足: (
(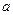 为常数,
为常数,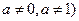
(1)求 的通项公式;
的通项公式;
(2)设 ,若数列
,若数列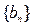 为等比数列,求
为等比数列,求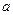 的值。
的值。