如图,已知四棱锥P﹣ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC=3,侧面PBC⊥底面ABCD,O是BC的中点.
(1)求证:DC∥平面PAB;
(2)求四棱锥P﹣ABCD的体积.
(Ⅰ)①证明两角和的余弦公式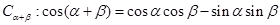 ;②由
;②由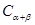 推导两角和的正弦公式
推导两角和的正弦公式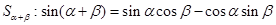
(Ⅱ)已知△ABC的面积 S=12,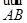 •
•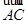 =3,且 cosB=
=3,且 cosB=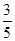 ,求cosC.
,求cosC.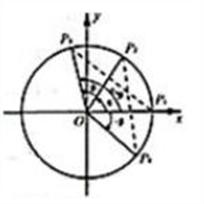
(本小题12分)已知函数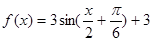
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出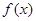 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;
(3)说明此函数图象可由 上的图象经怎样的变换得到.
上的图象经怎样的变换得到.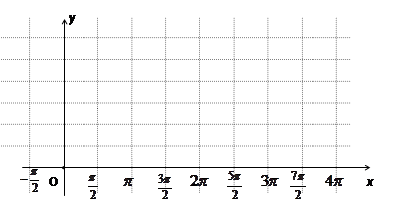
已知函数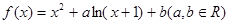 在点
在点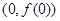 的切线方程为
的切线方程为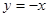
(1)求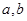 的值;
的值;
(2)当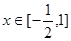 时,
时,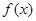 的图像与直线
的图像与直线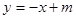 有两个不同的交点,求实数
有两个不同的交点,求实数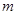 的取值范围;
的取值范围;
(3)证明对任意的正整数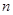 ,不等式
,不等式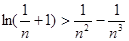 都成立.
都成立.
已知函数 (
(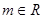 ),
), 的导数为
的导数为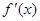 ,且
,且 的图像过点
的图像过点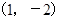
(1)求函数 的解析式;
的解析式;
(2)设函数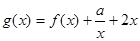 ,若
,若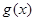 在
在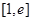 的最小值是2,求实数
的最小值是2,求实数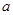 的值.
的值.
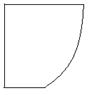
学校为扩大规模,把后山一块不规则的非农业用地规划建成一个矩形运动场地.已知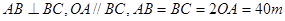 ,曲线段
,曲线段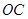 是以点
是以点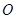 为顶点且开口向上的抛物线的一段(如图所示).如果要使矩形的相邻两边分别落在
为顶点且开口向上的抛物线的一段(如图所示).如果要使矩形的相邻两边分别落在 上,且一个顶点落在曲线段
上,且一个顶点落在曲线段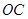 上,问应如何规划才能使运动场地面积最大?
上,问应如何规划才能使运动场地面积最大?