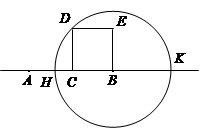如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
(Ⅰ)求异面直线EF与AG所成角的余弦值;
(Ⅱ)求证:BC∥面EFG;
(Ⅲ)求三棱锥E-AFG的体积.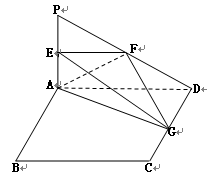
在等差数列 中,
中, ,其前
,其前 项和为
项和为 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数, ,公比为
,公比为 ,且
,且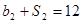 ,
,  .
.
(Ⅰ)求 与
与 ;(Ⅱ)设数列
;(Ⅱ)设数列 满足
满足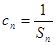 ,求
,求 的前
的前 项和
项和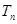
已知函数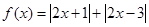
(Ⅰ)求不等式 ≤6的解集;
≤6的解集;
(Ⅱ)若关于x的不等式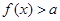 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
以直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,并在两种坐标系中取相同的单位长度.已知直线l的极坐标方程为 ,曲线C的参数方程为
,曲线C的参数方程为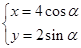 (α为参数).
(α为参数).
(Ⅰ)求直线l的直角坐标方程和曲线C的普通方程;
(Ⅱ)若直线l与曲线C交于A、B两点,求线段AB的长
如图,设C为线段AB的中点,BCDE是以BC为一边的正方形,以B为圆心,BD为半径的圆与AB及其延长线相交于点H及K.
(Ⅰ)求证:HC·CK=BC2;
(Ⅱ)若圆的半径等于2,求AH·AK的值.