以直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,并在两种坐标系中取相同的单位长度.已知直线l的极坐标方程为 ,曲线C的参数方程为
,曲线C的参数方程为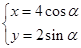 (α为参数).
(α为参数).
(Ⅰ)求直线l的直角坐标方程和曲线C的普通方程;
(Ⅱ)若直线l与曲线C交于A、B两点,求线段AB的长
(本小题满分14分)某工厂统计资料显示,一种产品次品率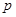 与日产量
与日产量 件之间的关系如下表所示:
件之间的关系如下表所示:
日产量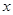 |
80 |
81 |
82 |
… |
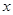 |
… |
98 |
99 |
100 |
次品率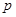 |
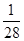 |
 |
 |
… |
P(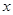 ) ) |
… |
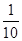 |
 |
 |
其中 (
(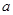 为常数).已知生产一件正品盈利
为常数).已知生产一件正品盈利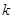 元,生产一件次品损失
元,生产一件次品损失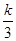 元(
元(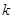 为给定常数).(Ⅰ)求出
为给定常数).(Ⅰ)求出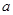 ,并将该厂的日盈利额
,并将该厂的日盈利额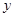 (元)表示为日生产量
(元)表示为日生产量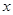 (件)的函数;
(件)的函数;
(Ⅱ)为了获得最大盈利,该厂的日生产量应该定为多少件?
(本小题满分14分)如图,单位圆(半径为1的圆)的圆心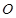 为坐标原点,单位圆与
为坐标原点,单位圆与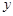 轴的正半轴交与点
轴的正半轴交与点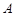 ,与钝角
,与钝角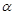 的终边
的终边 交于点
交于点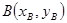 ,设
,设 .
.
(Ⅰ)用 表示
表示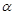 ;
;
(Ⅱ)如果 ,求点
,求点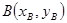 的坐标;
的坐标;
(Ⅲ)求 的最小值.
的最小值.
(本小题满分14分)如图,在四棱锥 中,底面
中,底面 为菱形,
为菱形,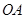 ⊥平面
⊥平面 ,
, 为
为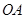 的中点,
的中点, 为
为 的中点,
的中点,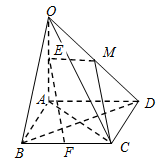
求证:(Ⅰ)平面 ⊥平面
⊥平面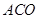 ;(Ⅱ)
;(Ⅱ)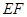 //平面
//平面 .
.
)已知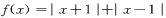 ,不等式
,不等式 的解集为M.
的解集为M.
(I)求M;
(II)当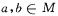 时,证明:
时,证明: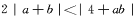 .
.
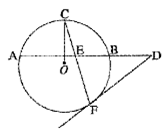
如图,AB是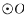 的弦,C、F是
的弦,C、F是 上的点,OC垂直于弦AB,过点F作
上的点,OC垂直于弦AB,过点F作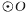 的切线,交AB的延长线于D,连结CF交AB于点E.
的切线,交AB的延长线于D,连结CF交AB于点E.
(I) 求证: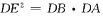 ;
;
(II)若BE = 1,DE = 2AE,求 DF 的长.