如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
(Ⅰ)求异面直线EF与AG所成角的余弦值;
(Ⅱ)求证:BC∥面EFG;
(Ⅲ)求三棱锥E-AFG的体积.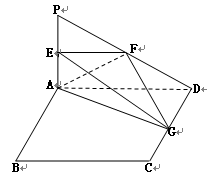
在复平面内,复数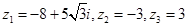 所对应的点为
所对应的点为 、
、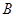 、
、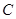 ,以
,以 、
、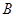 、
、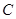 为顶点的三角形为
为顶点的三角形为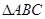
(1)求 ;
;
(2)求以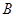 、
、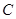 为焦点且过点
为焦点且过点 的双曲线的方程.
的双曲线的方程.
已知函数 ,其中
,其中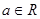 ,
,
(1)当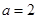 时,把函数
时,把函数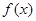 写成分段函数的形式;
写成分段函数的形式;
(2)当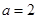 时,求
时,求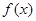 在区间[1,3]上的最值;
在区间[1,3]上的最值;
(3)设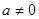 ,函数
,函数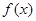 在开区间
在开区间 上既有最大值又有最小值,请分别求出
上既有最大值又有最小值,请分别求出 的取值范围(用
的取值范围(用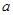 表示)
表示)
设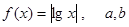 为实数,且
为实数,且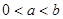 .
.
(1)求方程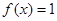 的解;
的解;
(2)若 ,
, 满足
满足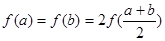 ,
,
求证:(1)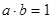 ;
;
(2) .
.
(3)在(2)的条件下,求证:由关系式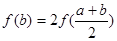 所得到的关于
所得到的关于 的方程
的方程 ,
,
存在 ,使
,使 .
.
已知函数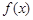 在
在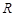 上为增函数,且过
上为增函数,且过 和
和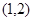 两点,集合
两点,集合 ,关于
,关于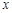 的不等式
的不等式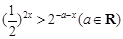 的解集为
的解集为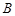 ,求使
,求使 的实数
的实数 的取值范围.
的取值范围.
函数 为常数,
为常数,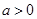 且
且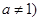 的图象过点
的图象过点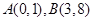
(1)求函数 的解析式;
的解析式;
(2)若函数 是奇函数,求
是奇函数,求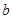 的值;
的值;