(本题满分12分)
投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分.现知某人在以前投掷1000次的试验中,有500次入红袋,250次入蓝袋,其余不能入袋
(1)求该人在4次投掷中恰有三次投入红袋的概率;
(2) 求该人两次投掷后得分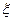 的分布列和数学期望.
的分布列和数学期望.
(本小题满分14分)水库的储水量随时间而变化,现用t表示时间,以月为单位,以年初为起点,根据历年数据,某水库的储水量(单位:亿立方米)关于t的近似函数关系式为: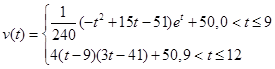
(1)该水库的储水量小于50的时期称为枯水期。以 表示第i个月份(i=1,2,...,12),问:一年内哪几个月份是枯水期?
表示第i个月份(i=1,2,...,12),问:一年内哪几个月份是枯水期?
(2)求一年内该水库的最大储水量(取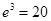 计算)
计算)
(本小题满分14分)已知函数 其中向量
其中向量

 若
若 的图像上相邻两个对称中心的距离大于等于
的图像上相邻两个对称中心的距离大于等于
(1)求 的取值范围;
的取值范围;
(2)在 中,
中, 分别是角
分别是角 的对边,
的对边, 当
当 最大时,
最大时, 求
求 的面积最大值.
的面积最大值.
(本小题满分14分)如图,在直三棱柱 中,
中, 、
、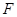 分别是
分别是 、
、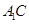 的中点,点
的中点,点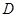 在
在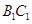 上,
上, 。
。
求证:(1) 平面ABC;
平面ABC;
(2)平面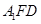
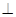 平面
平面 .
.
已知函数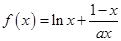 ,其中
,其中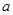 为大于零的常数.
为大于零的常数.
(Ⅰ)当a=1时,求函数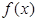 的单调区间,
的单调区间,
(Ⅱ)求函数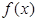 在区间[1,2]上的最小值;
在区间[1,2]上的最小值;
(Ⅲ)求证:对于任意的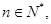 n>1时,都有
n>1时,都有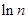 >
> 成立.
成立.
已知定理:“若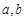 为常数,
为常数,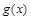 满足
满足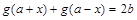 ,则函数
,则函数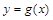 的图象关于点
的图象关于点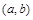 中心对称”.设函数
中心对称”.设函数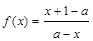 ,定义域为A.
,定义域为A.
(1)试证明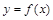 的图象关于点
的图象关于点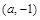 成中心对称;
成中心对称;
(2)当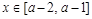 时,求证:
时,求证: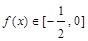 ;
;
(3)对于给定的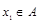 ,设计构造过程:
,设计构造过程: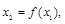
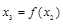 ,…,
,…,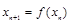 .如果
.如果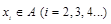 ,构造过程将继续下去;如果
,构造过程将继续下去;如果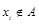 ,构造过程将停止.若对任意
,构造过程将停止.若对任意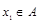 ,构造过程可以无限进行下去,求a的值.
,构造过程可以无限进行下去,求a的值.