已知定理:“若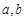 为常数,
为常数,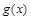 满足
满足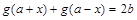 ,则函数
,则函数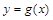 的图象关于点
的图象关于点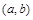 中心对称”.设函数
中心对称”.设函数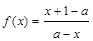 ,定义域为A.
,定义域为A.
(1)试证明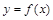 的图象关于点
的图象关于点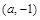 成中心对称;
成中心对称;
(2)当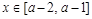 时,求证:
时,求证: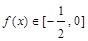 ;
;
(3)对于给定的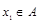 ,设计构造过程:
,设计构造过程: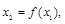
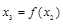 ,…,
,…,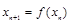 .如果
.如果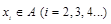 ,构造过程将继续下去;如果
,构造过程将继续下去;如果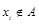 ,构造过程将停止.若对任意
,构造过程将停止.若对任意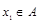 ,构造过程可以无限进行下去,求a的值.
,构造过程可以无限进行下去,求a的值.
(本小题满分10分)选修4—5:不等式选讲
(I)已知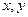 都是正实数,求证:
都是正实数,求证: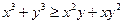 ;
;
(II)已知 都是正实数,求证:
都是正实数,求证: .
.
(本小题满分10分)选修4—4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的 轴的正半轴重合.直线
轴的正半轴重合.直线 的参数方程是
的参数方程是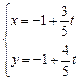 (
(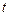 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为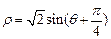 .
.
(I)求曲线 的直角坐标方程;
的直角坐标方程;
(II)设直线 与曲线
与曲线 相交于
相交于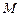 ,
, 两点,求M,N两点间的距离
两点,求M,N两点间的距离
(本小题满分10分)选修4—1:几何证明选讲
如图所示,AB是⊙O的直径,G为AB延长线上的一点,GCD是⊙O的割线,过点(
G作AB的垂线,交AC的延长线于点E,交AD的延长线于点F,过G作⊙O的切线,切点为H .求证: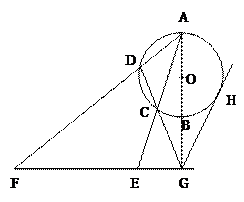
(I)C,D,F,E四点共圆;
(II)GH2=GE·GF.
(本小题满分12分)
已知函数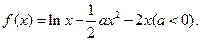
(1)若函数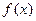 在定义域内单调递增,求
在定义域内单调递增,求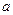 的取值范围;
的取值范围;
(2)若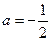 且关于x的方程
且关于x的方程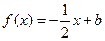 在
在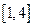 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数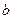 的取值范围;
的取值范围;
(3)设各项为正的数列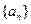 满足:
满足: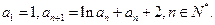 求证:
求证: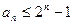
(本小题满分12分)
如图,正方形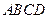 所在平面与圆
所在平面与圆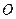 所在平面相交于
所在平面相交于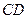 ,线段
,线段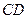 为圆
为圆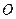 的弦,
的弦,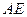 垂直于圆
垂直于圆 所在平面,垂足
所在平面,垂足 是圆
是圆 上异于
上异于 .
.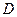 的点,
的点, ,圆
,圆 的直径为9.
的直径为9.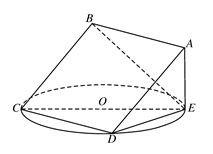
(I)求证:平面 平面
平面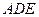 ;
;
(II)求二面角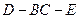 的平面角的正切值.
的平面角的正切值.