在以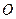 为原点的直角坐标系中,点
为原点的直角坐标系中,点 为
为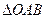 的直角顶点,若
的直角顶点,若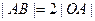 ,且点
,且点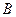 的纵坐标大于0
的纵坐标大于0
(1)求向量 的坐标;
的坐标;
(2)是否存在实数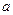 ,使得抛物线
,使得抛物线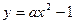 上总有关于直线
上总有关于直线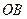 对称的两个点?若存在,求实数
对称的两个点?若存在,求实数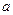 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
(本小题满分12分)
已知直线l:y=x,圆C1的圆心为(3,0),且经过(4,1)点.
(1)求圆C1的方程;
(2)若圆C2与圆C1关于直线l对称,点A、B分别为圆C1、C2上任意一点,求|AB|的最小值;
(3)已知直线l上一点M在第一象限,两质点P、Q同时从原点出发,点P以每秒1个单位的速度沿x轴正方向运动,点Q以每秒 个单位沿射线OM方向运动,设运动时间为t秒.问:当t为何值时直线PQ与圆C1相切?
个单位沿射线OM方向运动,设运动时间为t秒.问:当t为何值时直线PQ与圆C1相切?
(本小题满分12分)
已知圆C的方程为x2+y2=4.
(1)求过点P(1,2)且与圆C相切的直线l的方程;
(2)直线l过点P(1,2),且与圆C交于A、B两点,若|AB|=2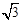 ,求直线l的方程.
,求直线l的方程.
(本小题满分12分)
正方体ABCD-A1B1C1D1中,E、G分别是BC、C1D1的中点,如图所示.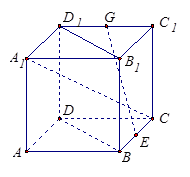
(1)求证:BD⊥A1C;
(2)求证:EG∥平面BB1D1D.
(本小题满分12分)
下列三个图中,左边是一个正方体截去一个角后所得多面体的直观图。右边两个是正视图和侧视图.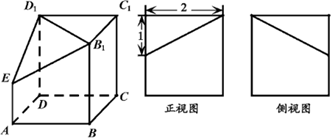
(1)请在正视图的下方,按照画三视图的要求画出该多面体的俯视图(不要求叙述作图过程);
(2)求该多面体的体积(尺寸如图).
(本小题满分12分)
已知直线l1经过A(1,1)和B(3,2),直线l2方程为2x-4y-3=0.
(1)求直线l1的方程;
(2)判断直线l1与l2的位置关系,并说明理由。