(本小题满分12分)
已知圆C的方程为x2+y2=4.
(1)求过点P(1,2)且与圆C相切的直线l的方程;
(2)直线l过点P(1,2),且与圆C交于A、B两点,若|AB|=2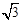 ,求直线l的方程.
,求直线l的方程.
(本小题满分12分)
如图,已知正三棱柱ABC—A1B1C1的底面边长是2,D是CC1的中点,直线AD与侧面BB1C1C所成的角是45°.
(I)求二面角A—BD—C的大小;
(II)求点C到平面ABD的距离.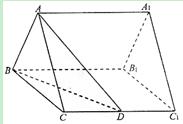
(本小题满分10分)
已知A,B,C是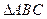 的三个内角,向量
的三个内角,向量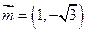 ,
,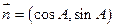 ,且
,且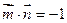 .
.
(I)求角A;
(II)若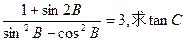 的值.
的值.
(本小题满分10分)
已知函数f(x)= m·log2x + t的图象经过点A(4,1)、点B(16,3)及点C(Sn,n),其中Sn为数列{an}的前n项和,n∈N*.
(Ⅰ)求Sn和an;
(Ⅱ)设数列{bn}的前n项和为Tn , bn = f(an) – 1, 求不等式Tn£ bn的解集,n∈N*.
(本小题满分10分)
已知向量 ,
, ,
,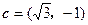 ,其中
,其中 .
.
(Ⅰ)当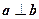 时,求
时,求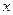 值的集合; (Ⅱ)求
值的集合; (Ⅱ)求 的最大值.
的最大值.
(本小题满分10分)
已知
(Ⅰ)若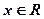 ,求f(x)的单调增区间;
,求f(x)的单调增区间;
(Ⅱ)若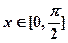 时,f(x)的最大值为4,求a的值.
时,f(x)的最大值为4,求a的值.