如图,圆柱 内有一个三棱柱
内有一个三棱柱 ,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径。
,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径。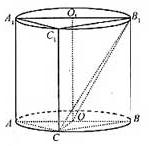
(Ⅰ)证明:平面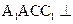 平面
平面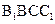 ;
;
(Ⅱ)设AB=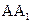 ,在圆柱
,在圆柱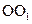 内随机选取一点,记该点取自于三棱柱
内随机选取一点,记该点取自于三棱柱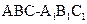 内的概率为
内的概率为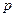 。
。
(i)当点C在圆周上运动时,求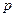 的最大值;
的最大值;
(ii)记平面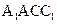 与平面
与平面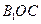 所成的角为
所成的角为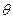
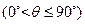 ,当
,当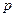 取最大值时,求
取最大值时,求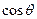 的值。
的值。
已知抛物线的顶点在原点,焦点在y轴的负半轴上,过其上一点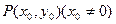 的切线方程为
的切线方程为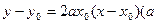 为常数).
为常数).
(I)求抛物线方程;
(II)斜率为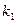 的直线PA与抛物线的另一交点为A,斜率为
的直线PA与抛物线的另一交点为A,斜率为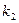 的直线PB与抛物线的另一交点为B(A、B两点不同),且满足
的直线PB与抛物线的另一交点为B(A、B两点不同),且满足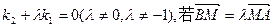 ,求证线段PM的中点在y轴上;
,求证线段PM的中点在y轴上;
(III)在(II)的条件下,当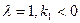 时,若P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标的取值范围.
时,若P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标的取值范围.
设椭圆 的左、右焦点分别为
的左、右焦点分别为 、
、 ,A是椭圆C上的一点,且
,A是椭圆C上的一点,且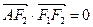 ,坐标原点O到直线
,坐标原点O到直线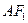 的距离为
的距离为 .
.
(1)求椭圆C的方程;
(2)设Q是椭圆C上的一点,过Q的直线l交x轴于点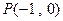 ,较y轴于点M,若
,较y轴于点M,若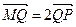 ,求直线l的方程.
,求直线l的方程.
已知定点A(-2,0),动点B是圆 (F为圆心)上一点,线段AB的垂直平分线交BF于P.
(F为圆心)上一点,线段AB的垂直平分线交BF于P.
(1)求动点P的轨迹方程;
(2)是否存在过点E(0,-4)的直线l交P点的轨迹于点R,T,且满足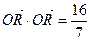 (O为原点),若存在,求直线l的方程,若不存在,请说明理由.
(O为原点),若存在,求直线l的方程,若不存在,请说明理由.
已知 ,动点
,动点 满足
满足 .
.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过点 作直线
作直线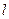 与曲线
与曲线 交于
交于 两点,若
两点,若 ,求直线
,求直线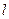 的方程;
的方程;
(Ⅲ)设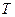 为曲线
为曲线 在第一象限内的一点,曲线
在第一象限内的一点,曲线 在
在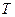 处的切线与
处的切线与
 轴分别交于点
轴分别交于点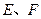 ,求
,求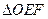 面积的最小值.
面积的最小值.
已知抛物线y=x2上的两点A、B满足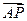 =l
=l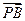 ,l>0,其中点P坐标为(0,1),
,l>0,其中点P坐标为(0,1), =
= +
+ ,O为坐标原点.
,O为坐标原点.
(I)求四边形OAMB的面积的最小值;
(II)求点M的轨迹方程.