已知数列 前项和
前项和 且
且 ,
,
(1)试求
(2)猜想 的表达式,并用数学归纳法证明猜想.
的表达式,并用数学归纳法证明猜想.
已知 是复数,若
是复数,若 为实数(
为实数( 为虚数单位),且
为虚数单位),且 为纯虚数.
为纯虚数.
(1)求复数 ;
;
(2)若复数 在复平面上对应的点在第四象限,求实数
在复平面上对应的点在第四象限,求实数 的取值范围
的取值范围
已知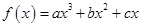 在区间
在区间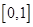 上是增函数,在区间
上是增函数,在区间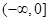 和
和 上是减函数,且
上是减函数,且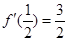
(1)求函数 的解析式.
的解析式.
(2)若在区间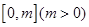 上恒有
上恒有 ,求实数
,求实数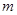 的取值范围.
的取值范围.
现有0,1,2,3,4,5六个数字。
(1)用所给数字能够组成多少个四位数?
(2)用所给数字可以组成多少个没有重复数字的五位数?
(3)用所给数字可以组成多少个没有重复数字且比3142大的数?(最后结果均用数字作答)
已知函数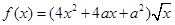 ,其中
,其中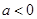 .
.
(1)当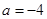 时,求
时,求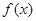 的单调递增区间;
的单调递增区间;
(2)若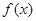 在区间
在区间 上的最小值为8,求
上的最小值为8,求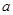 的值.
的值.