如图所示，位于竖直平面内的光滑轨道，由一段斜的直轨道和与之相切的圆形轨道连
接而成，圆形轨道得半径为R．一质量为m的小物块从斜轨道上某处由静止开始下滑，然
后沿圆形轨道运动．要求物块能通过圆形轨道最高点，且在该最高点与轨道间的压力不能
超过５mg(g为重力加速度)，求物块初始位置相对于圆形轨道底部的高度h的取值范围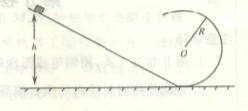
某兴趣小组对一辆自制遥控小车的性能进行研究。他们让这辆小车在水平的直轨道上由静止开始运动，并将小车运动的全过程记录下来，通过处理转化为v—t图象，如图所示（除2s—10s时间段图象为曲线外，其余时间段图象均为直线）。已知
在小车运动的过程中，2s—14s时间段内小车的功率保持不变，在14s末停止遥控而让小车自由滑行，小车的质量为1.0kg，可认为在整个运动过程中小车所受到的阻力大小不变。求：
小车所受到的阻力大小；
小车匀速行驶阶段的功率；
小车在加速运动过程中位移的大小。
站立在地面上的质量分别为M和M+m的两个人，分别拉住定滑轮两边的绳子往上爬。开始时，两人与定滑轮的距离都是h，如图所示，设滑轮和绳子的质量及滑轮轴处的摩擦均不计, 且人施加于绳子的力恒定。问：当质量小的人在时间t内爬到滑轮时，
质量大的人与滑轮间的距离是多大？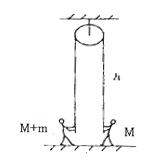
如图，真空中有一匀强电场，方向沿Ox正方向，若质量为m、电荷量为q的带电微粒从O点以初速v0沿Oy方向进入电场，经Δt时间到达A点，此时速度大小也是vo，方向沿Ox轴正方向，如图所示。求：
从O点到A点的时间Δt。
该匀强电场的场强E及OA连线与Ox轴的夹角θ。
若设O点电势为零，则A点电势多大。
如图所示，在点电荷＋Q的电场中有A、B两点，将质子和α粒子分别从A点由静止释放到达B点时，它们的速度大小之比是多少？
如右图所示，电源电动势E="10" V，内阻r=0.5Ω，标有“8 V,16 W”的灯泡恰好能正常发光，电动机M绕组的电阻R0=1Ω，求：
通过电源的电流；
电源的输出功率；
电动机的输出功率。