如图,已知椭圆
过点
,离心率为
,左右焦点分别为
.点
为直线
:
上且不在
轴上的任意一点,直线
和
与椭圆的交点分别为
和
.
为坐标原点.
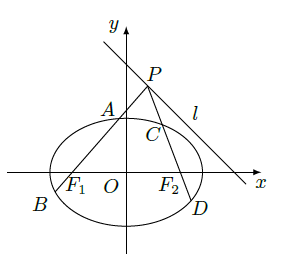
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设直线
斜率分别为
.
(ⅰ)证明:
(ⅱ)问直线 上是否存在一点 ,使直线 的斜率 满足 ?若存在,求出所有满足条件的点 的坐标;若不存在,说明理由.
已知全集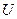 为
为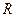 ,集合
,集合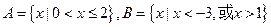
求:(1)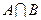 (2)
(2)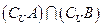 ;(3)
;(3)
(本题10分)如图,已知点A(2,3), B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上
(Ⅰ)求AB边上的高CE所在直线的方程
(Ⅱ)求△ABC的面积
(本小题满分12分)
已知函数f(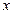 )=
)=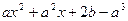 ,当
,当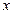 ∈(-2,6)时,其值为正,而当
∈(-2,6)时,其值为正,而当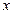 ∈(-∞,-2)∪(6,+∞)时,其值为负
∈(-∞,-2)∪(6,+∞)时,其值为负
(I)求实数 的值及函数f(
的值及函数f(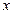 )的解析式
)的解析式
(II)设F(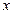 )= -
)= -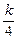 f(
f(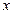 )+4
)+4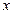 +12
+12 ,问
,问 取何值时,方程F(
取何值时,方程F(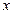 )=0有正根?
)=0有正根?
(本小题满分12分)
已知等比数列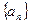 的各项均为正数,且
的各项均为正数,且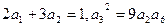
(I)求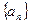 的通项公式
的通项公式
(II)令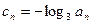 ,求数列
,求数列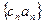 的前n项和
的前n项和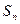
(本题12分)如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,M为线段AB的中点,将△ACD沿 折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
(Ⅰ)求证:BC⊥平面ACD;
(Ⅱ)求二面角A-CD-M的余弦值.