(本小题满分12分)如图,在直三棱柱ABC—A1B1C1中,∠ACB=90°,AC=BC=CC1=2.
(I)证明:AB1⊥BC1;
(II)求点B到平面AB1C1的距离;
(III)求二面角C1—AB1—A1的大小.
求直线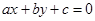 的倾斜角
的倾斜角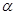 .(若
.(若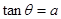 ,则有
,则有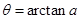 )
)
如图,在四棱锥P-ABCD中,四边形ABCD是矩形,侧面PAD⊥底面ABCD,若点E,F分别是PC,BD的中点。
(1)求证:EF∥平面PAD;
(2)求证:平面PAD⊥平面PCD
如图,在梯形ABCD中,AB∥CD,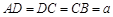 ,
,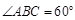 ,平面
,平面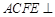 平面
平面 ,四边形
,四边形 是矩形,
是矩形,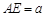 ,点
,点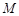 在线段
在线段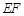 上。
上。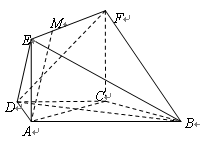
(1)求证: 平面
平面 ;
;
(2)当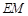 为何值时,
为何值时,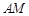 ∥平面
∥平面 ?写出结论,并加以证明;
?写出结论,并加以证明;
(3)当EM为何值时,AM⊥BE?写出结论,并加以证明。
【改编】在正四棱柱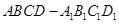 中,已知底面
中,已知底面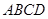 的边长为2,点P是
的边长为2,点P是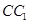 的中点,且
的中点,且 .
.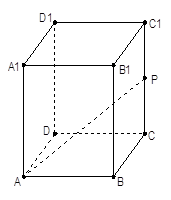
(1)求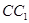 的长;
的长;
(2)求点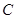 到平面
到平面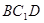 的距离.
的距离.
【原创】(1),已知: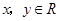 ,且满足
,且满足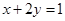 ,求
,求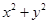 的最小值;
的最小值;
(2),已知: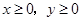 ,且满足
,且满足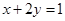 ,求
,求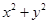 的最大值.
的最大值.