如图,在梯形ABCD中,AB∥CD,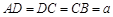 ,
,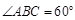 ,平面
,平面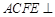 平面
平面 ,四边形
,四边形 是矩形,
是矩形,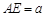 ,点
,点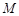 在线段
在线段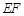 上。
上。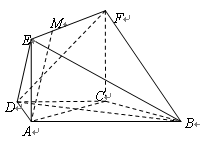
(1)求证: 平面
平面 ;
;
(2)当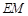 为何值时,
为何值时,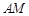 ∥平面
∥平面 ?写出结论,并加以证明;
?写出结论,并加以证明;
(3)当EM为何值时,AM⊥BE?写出结论,并加以证明。
已知函数f(x)=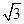 cos2x+sinxcosx
cos2x+sinxcosx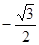 .
.
(1)求函数f(x)的单调递增区间;
(2)若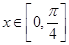 ,求函数f(x)的取值范围;
,求函数f(x)的取值范围;
(本小题满分14分)设数列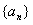 的首项
的首项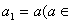 R),且
R),且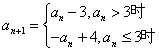 ,
,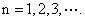 (Ⅰ)若
(Ⅰ)若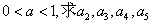 ;(Ⅱ)若
;(Ⅱ)若 ,证明:
,证明: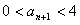 ;(Ⅲ)若
;(Ⅲ)若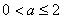 ,求所有的正整数
,求所有的正整数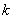 ,使得对于任意
,使得对于任意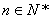 ,均有
,均有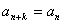 成立.
成立.
(本小题满分14分)
已知函数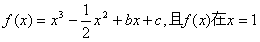 处取得极值.
处取得极值.
(Ⅰ)求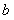 的值;
的值;
(Ⅱ)若当 恒成立,求
恒成立,求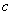 的取值范围;
的取值范围;
(Ⅲ)对任意的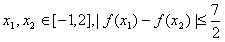 是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
(本小题满分13分)已知各项都不相等的等差数列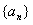 的前六项和为60,且
的前六项和为60,且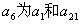 的等比中项.(Ⅰ)求数列
的等比中项.(Ⅰ)求数列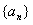 的通项公式
的通项公式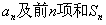 ;(Ⅱ)若数列
;(Ⅱ)若数列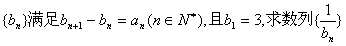 的前
的前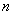 项和
项和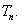
(本小题满分13分)如图,正三棱柱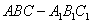 中,D是BC的中点,
中,D是BC的中点,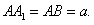
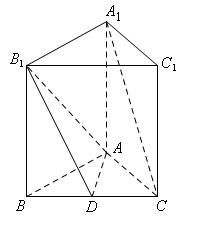
(Ⅰ)求证: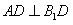 ;(Ⅱ)求证:
;(Ⅱ)求证: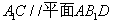 ;(Ⅲ)求三棱锥
;(Ⅲ)求三棱锥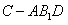 的体积.
的体积.