(本小题15分)若关于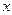 的不等式
的不等式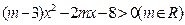 的解集是一个开区间
的解集是一个开区间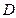 ,定义开区间
,定义开区间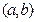 的长度
的长度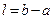 。
。
(1)求开区间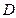 的长度
的长度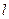 (
(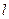 用
用 表示),并写出其定义域;
表示),并写出其定义域;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.
已知函数 ,其定义域为
,其定义域为 ,最大值为6.
,最大值为6.
(1)求常数m的值;
(2)求函数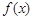 的单调递增区间.
的单调递增区间.
已知函数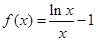 .
.
(1)试判断函数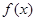 的单调性;
的单调性;
(2)设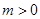 ,求
,求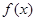 在
在 上的最大值;
上的最大值;
(3)试证明:对任意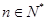 ,不等式
,不等式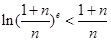 都成立(其中
都成立(其中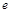 是自然对数的底数).
是自然对数的底数).
如图,已知椭圆 的左、右焦点分别
的左、右焦点分别
为 ,其上顶点为
,其上顶点为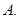 已知
已知 是边长为
是边长为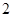 的正三角形.
的正三角形.
(1)求椭圆 的方程;
的方程;
(2)过点 任作一动直线
任作一动直线 交椭圆
交椭圆 于
于 两点,记
两点,记 .若在线段
.若在线段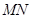 上取一点
上取一点 ,使得
,使得 ,当直线
,当直线 运动时,点
运动时,点 在某一定直线上运动,求出该定直线的方程.
在某一定直线上运动,求出该定直线的方程.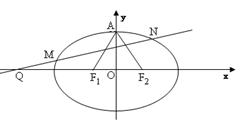
空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,解代表空气污染越严重:
| PM2.5日均浓度 |
0~35 |
35~75 |
75~115 |
115~150 |
150~250 |
>250 |
| 空气质量级别 |
一级 |
二级 |
三级 |
四级 |
五级 |
六级 |
| 空气质量类别 |
优 |
良 |
轻度污染 |
中度污染 |
重度污染 |
严重污染 |

某市2013年3月8日—4月7日(30天)对空气质量指数PM2.5进行检测,获得数据后整理得到如下条形图:
(1)估计该城市一个月内空气质量类别为良的概率;
(2)从空气质量级别为三级和四级的数据中任取2个,求至少有一天空气质量类别为中度污染的概率.
已知等差数列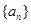 的首项
的首项 ,公差
,公差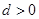 ,且第
,且第 项、第
项、第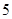 项、第
项、第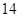 项分别是等比数列
项分别是等比数列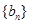 的第
的第 项、第
项、第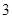 项、第
项、第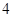 项.
项.
(1)求数列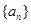 ,
,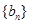 的通项公式;
的通项公式;
(2)若数列 对任意
对任意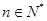 ,均有
,均有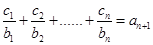 成立.
成立.
①求证: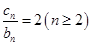 ;②求
;②求 .
.