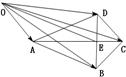
已知四边形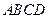 ,
,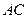 是
是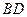 的垂直平分线,垂足
的垂直平分线,垂足
为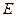 ,
,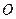 为直线
为直线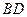 外一点.设向量
外一点.设向量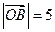 ,
,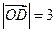 ,
,
则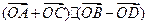 的值是( )
的值是( )
A.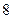 |
B.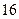 |
C.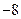 |
D.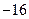 |
 |
观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a10+b10=( )
| A.28 | B.76 | C.123 | D.199 |
四个小动物换座位,开始是猴、兔、猫、鼠分别坐在1、2、3、4号位置上(如图),第1次前后排动物互换位置,第2次左右列互换座位,……这样交替进行下去,那么第2014次互换座位后,小兔的位置对应的是( )
| A.编号1 | B.编号2 | C.编号3 | D.编号4 |
三段论推理“①矩形是平行四边形;②三角形不是平行四边形;③三角形不是矩形”中的小前提是( )
| A.① | B.② | C.③ | D.①和② |
已知b>0,直线(b2+1)x+ay+2=0与直线x-b2y-1=0互相垂直,则ab的最小值等于( )
| A.1 | B.2 | C.2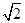 |
D.2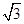 |
已知a>0,b>0,若不等式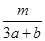 -
-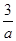 -
-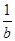 ≤0恒成立,则m的最大值为( )
≤0恒成立,则m的最大值为( )
| A.4 | B.16 | C.9 | D.3 |