(附加题)将一个半径适当的小球放入如图所示的容器最上方的入口处, 小球将自由下落.小球在下落过程中,将3次遇到黑色障碍物,最后落入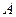 袋或
袋或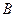 袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是.
袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是.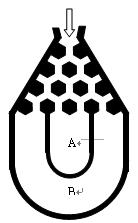
(Ⅰ)求小球落入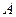 袋中的概率
袋中的概率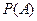 ;
;
(Ⅱ)在容器入口处依次放入4个小球,记X为落入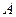 袋中小球的个数,试求X=3的概率和X的数学期望
袋中小球的个数,试求X=3的概率和X的数学期望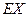 .
.
在直三棱柱ABC﹣A1B1C1中,BC=CC1,AB⊥BC.点M,N分别是CC1,B1C的中点,G是棱AB上的动点.
(Ⅰ)求证:B1C⊥平面BNG;
(Ⅱ)若CG∥平面AB1M,试确定G点的位置,并给出证明.
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
(Ⅰ)求证:AB∥平面DEG;
(Ⅱ)求证:BD⊥EG.
求经过点A(5,2),B(3,2),圆心在直线2x﹣y﹣3=0上圆的标准方程.
如图,已知三棱柱ABC﹣A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱CC1到点A1的最短路线长为2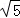 ,设这条最短路线与交于点D.
,设这条最短路线与交于点D.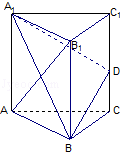
(1)求三棱柱ABC﹣A1B1C1的棱长;
(2)求四棱锥A1﹣BCC1B1的体积;
(3)在平面A1BD内是否存在过点D的直线与平面ABC平行?并说明理由.
(Ⅰ)求过点(1,﹣1),且与直线x+4y﹣7=0垂直的直线方程.
(Ⅱ)求过点(1,﹣1),且与直线x+4y﹣7=0平行的直线方程.