(本小题满分14分)已知{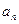 }(
}( 是正整数)是首项是
是正整数)是首项是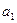 ,公比是
,公比是 的等比数列.
的等比数列.
(1)求和: ;
;
(2)由(1)的结果归纳概括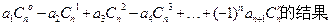
并加以证明;
(3)设 是等比数列的前
是等比数列的前 项的和,求
项的和,求
(本小题满分14分)已知数列 是递增数列,且满足
是递增数列,且满足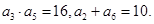
(Ⅰ)若 是等差数列,求数列
是等差数列,求数列 的通
的通 项公式;
项公式;
(Ⅱ)对于(Ⅰ)中 ,令
,令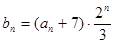 ,求数列
,求数列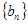 的前
的前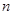 项和
项和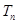 .
.
(本小题满分14分)在钝角三角形ABC中,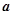 、
、 、
、 分别是角A、B、C的对边,
分别是角A、B、C的对边,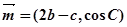 ,
,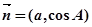 ,且
,且 ∥
∥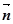 .
.
(Ⅰ)求角A的大小;
(Ⅱ)求函数 的值域.
的值域.
已知双曲线方程为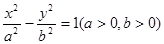 ,椭圆C以该双曲线的焦点为顶点,顶点为焦点。
,椭圆C以该双曲线的焦点为顶点,顶点为焦点。
(1)当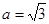 ,
, 时,求椭圆C的方程;
时,求椭圆C的方程;
(2)在(1)的条件下,直线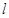 :
: 与
与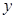 轴交于点P,与椭圆交与A,B两点,若O为坐标原点,
轴交于点P,与椭圆交与A,B两点,若O为坐标原点,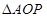 与
与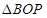 面积之比为2:1,求直线
面积之比为2:1,求直线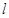 的方程;
的方程;
(3)若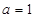 ,椭圆C与直线
,椭圆C与直线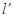 :
: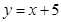 有公共点,求该椭圆的长轴长的最小值。
有公共点,求该椭圆的长轴长的最小值。
动圆C的方程为 。
。
(1)若 ,且直线
,且直线 与圆C交于A,B两点,求弦长
与圆C交于A,B两点,求弦长 ;
;
(2)求动圆圆心C的轨迹方程;
(3)若直线 与动圆圆心C的轨迹有公共点,求
与动圆圆心C的轨迹有公共点,求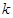 的取值范围。
的取值范围。
曲线C是平面内与两个定点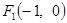 和
和 的距离的积等于常数
的距离的积等于常数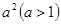
的点的轨迹,给出下列三个结论:
①曲线C过坐标原点;
②曲线C关于坐标原点对称;
③若点P在曲线C上,则△ 的面积不大于
的面积不大于 。
。
其中,所有正确结论的序号为_________。