（本小题满分8分）己知集合
（1）求集合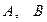
； （2）若
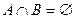,求实数
的取值范围。
写出命题“当
时，
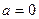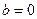或
或
”的逆命题、否命题、逆否命题，并判断其真假
一颗慧星沿一条以地球为焦点的抛物线运行时，当慧星离地球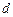
万公里时，经过地球和慧得的直线与抛物线对称轴的夹角为
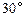，求此慧星运行时离地球的最近距离．
已知抛物线的顶点在原点，对称轴为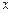
轴，抛物线上一点
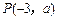到焦点的距离为5，求抛物线的标准方程．
求以原点为顶点，坐标轴为对称轴，并且经过点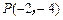
的抛物线的标准方程．
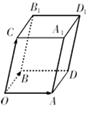
如图，已知向量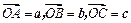
，可构成空间向量的一个基底，若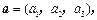
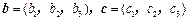，在向量已有的运算法则的基础上，新定义一种运算
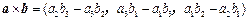，显然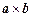
的结果仍为一向量，记作
．
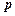（1）求证：向量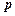为平面
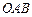的法向量；
（2）求证：以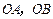
为边的平行四边形
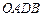的面积等于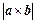
；
（3）将四边形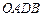按向量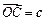
平移，得到一个平行六面体
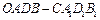，试判断平行六面体的体积
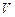与
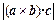的大小．