如图，已知向量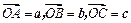
，可构成空间向量的一个基底，若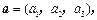
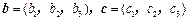，在向量已有的运算法则的基础上，新定义一种运算
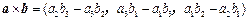，显然
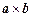的结果仍为一向量，记作
．
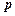（1） 求证：向量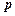为平面
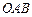的法向量；
（2） 求证：以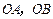
为边的平行四边形
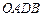的面积等于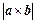
；
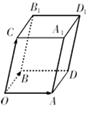
（3） 将四边形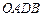按向量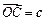
平移，得到一个平行六面体
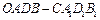，试判断平行六面体的体积
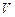与
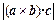的大小．
已知圆M经过直线l: 2x+y+4=0与圆C：x2+y2+2x－4y+1=0的交点，且圆M的圆心到直线2x+6y－5=0的距离为
，求圆M的方程
已知方程
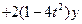
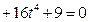表示一个圆。求t的取值范围；求该圆半径r的最大值及此时圆的标准方程
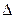ABC的三个顶点分别为A(－1,5)，(－2,－2),(5,5),求其外接圆方程
(本小题满分13分)已知函数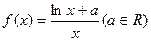
（Ⅰ）求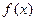
的极值；（Ⅱ）若函数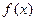的图象与函数
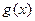=1的图象在区间
上有公共点，求实数a的取值范围
（本小题满分12分）
如图，直三棱柱A1B1C1—ABC中，C1C=CB=CA=2，AC⊥CB.
D、E分别为棱C1C、B1C1的中点.
(１)求二面角B—A1D—A的平面角余弦值；
(2)在线段AC上是否存在一点F，使得EF⊥平面A1BD？
若存在，确定其位置并证明结论；若不存在，说明理由.