.(本小题满分15分)
某校举行环保知识大奖赛，比赛分初赛和决赛两部分，初赛采用选手选一题答一题的方式进行，每位选手最多有5次选题答题的机会，选手累计答对3题或答错3题即终止其初赛的比赛，答对3题者直接进入决赛，答错3题者则被淘汰，已知选手甲回答每个问题的正确率相同，并且答题相互之间没有影响，且连续两次答错的概率为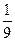
.
(1)求选手甲回答一个问题的正确率； (2)求选手甲进入决赛的概率；
(3)设选手甲在初赛中答题的个数为ξ，试写出ξ的分布列，并求ξ的数学期望.
已知不等式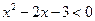
的解集为A，不等式
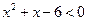的解集为B。
（1）求A∩B；
（2）若不等式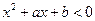
的解集为A∩B，求不等式
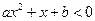的解集。
已知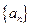
是等差数列，其中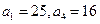
（1）求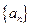的通项;
（2）数列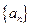从哪一项开始小于0;
（3）求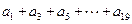
值。
甲、乙两名跳高运动员一次试跳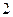
米高度成功的概率分别是
，
，且每次试跳成功与否相互之间没有影响，求：
（Ⅰ）甲试跳三次，第三次才成功的概率；
（Ⅱ）甲、乙两人在第一次试跳中至少有一人成功的概率；
（Ⅲ）甲、乙各试跳两次，甲比乙的成功次数恰好多一次的概率．
在医学生物学试验中，经常以果蝇作为试验对象.一个关有6只果蝇的笼子里，不慎混入了两只苍蝇（此时笼内共有8只蝇子：6只果蝇和2只苍蝇），只好把笼子打开一个小孔，让蝇子一只一只地往外飞，直到两只苍蝇都飞出，再关闭小孔.
(Ⅰ)求笼内恰好剩下1只果蝇的概率；
（Ⅱ）求笼内至少剩下5只果蝇的概率.
在医学生物学试验中，经常以果蝇作为试验对象，一个关有6只果蝇的笼子里，不慎混入了两只苍蝇（此时笼内共有8只蝇子：6只果蝇和2只苍蝇），只好把笼子打开一个小孔，让蝇子一只一只地往外飞，直到两只苍蝇都飞出，再关闭小孔.以ξ表示笼内还剩下的果蝇的只数.
（Ⅰ）写出ξ的分布列（不要求写出计算过程）；
（Ⅱ）求数学期望Eξ；
（Ⅲ）求概率P（ξ≥Eξ）.