在直角坐标系xoy中，椭圆C1：
的左、右焦点分别为F1、F2，F2也是抛物线C2：
的焦点，点M为C1与C2在第一象限的交点，且
。
（1）求C1的方程；
（2）平面上的点N满足
，直线
∥MN，且与C1交于A、B两点，若
，求直线的方程。
已知数列{an}的各项都是正数，且满足：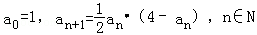
．
（1）求a1，a2；
（2）证明an＜an+1＜2，n∈N．
用数学归纳法证明不等式：
+
+
+…+
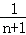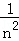＞1（n∈N*且n＞1）．
证明不等式
（n∈N*）
已知函数f（x）=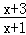
（x≠﹣1）．设数列{an}满足a1=1，an+1=f（an），数列{bn}满足bn=|an﹣
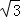|，Sn=b1+b2+…+bn（n∈N*）．
（Ⅰ）用数学归纳法证明bn≤
；
（Ⅱ）证明Sn＜
．
在数列|an|中，a1=t﹣1，其中t＞0且t≠1，且满足关系式：an+1（an+tn﹣1）=an（tn+1﹣1），（n∈N+）
（1）猜想出数列|an|的通项公式并用数学归纳法证明之；
（2）求证：an+1＞an，（n∈N+）．