（本小题满分14分）如图，正三棱柱ABC

已知是椭圆上两点，点M的坐标为.
（1）当两点关于轴对称，且为等边三角形时，求的长；
（2）当两点不关于轴对称时，证明：不可能为等边三角形.

已知曲线.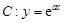
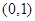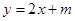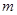(1)若曲线C在点处的切线为，求实数和的值；
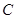(2)对任意实数，曲线总在直线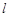: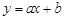的上方，求实数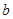的取值范围.

如图1，在Rt△ABC中，∠ACB=30°，∠ABC=90°，D为AC中点，于，延长AE交BC于F，将ABD沿BD折起，使平面ABD平面BCD，如图2所示.

（1）求证：AE⊥平面BCD；
（2）求二面角A–DC–B的余弦值．
（3）在线段上是否存在点使得平面？若存在,请指明点的位置；若不存在，请说明理由.

为了解甲、乙两个快递公司的工作状况，假设同一个公司快递员的工作状况基本相同，现从甲、乙两公司各随机抽取一名快递员，并从两人某月（30天）的快递件数记录结果中随机抽取10天的数据，制表如下：

甲公司某员工A		乙公司某员工B
3	9	6	5	8	3	3	2	3	4	6	6	6	7	7
						0	1	4	4	2	2	2

每名快递员完成一件货物投递可获得的劳务费情况如下：
甲公司规定每件4.5元；乙公司规定每天35件以内（含35件）的部分每件4元，超出35件的部分每件7元.
（1）根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数；
（2）为了解乙公司员工B的每天所得劳务费的情况，从这10天中随机抽取1天，他所得的劳务费记为（单位：元），求的分布列和数学期望；
（3）根据表中数据估算两公司的每位员工在该月所得的劳务费.

已知函数，过两点的直线的斜率记为.
（1）求的值；
（2）写出函数的解析式，求在上的取值范围.