通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设f (t)表示学生注意力随时间t(分钟)的变化规律(f(t)越大,表明学生注意力越集中),经过实验分析得知:
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
(本小题满分13分)根据新修订的《环境空气质量标准》指出空气质量指数在 ,各类人群可正常活动.某市环保局在2014年对该市进行为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为
,各类人群可正常活动.某市环保局在2014年对该市进行为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为 ,
, ,
, ,
, ,
, ,由此得到样本的空气质量指数频率分布直方图,如图.
,由此得到样本的空气质量指数频率分布直方图,如图.
(1)求 的值;
的值;
(2)根据样本数据,试估计这一年度的空气质量指数的平均值;
(3)用这50个样本数据来估计全年的总体数据,将频率视为概率.如果空气质量指数不超过20,就认定空气质量为“最优等级”.从这一年的监测数据中随机抽取2天的数值,其中达到“最优等级”的天数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分13分)已知函数 .
.
(1)求函数 的最小正周期和函数
的最小正周期和函数 的单调递增区间;
的单调递增区间;
(2)在 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,若
,若 ,
, ,
, 的面积为
的面积为 ,求边长
,求边长 的值.
的值.
(本题满分14分)已知椭圆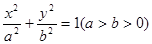 的离心率为
的离心率为 ,点P(1,
,点P(1, )在该椭圆上.
)在该椭圆上.
(1)求椭圆的标准方程;
(2)若直线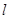 与圆O:
与圆O: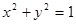 相切,并椭圆交于不同的两点A、B,求
相切,并椭圆交于不同的两点A、B,求
△AOB面积S的最大值.
(本题满分13分)已知函数 ,
, (a、b为常数).
(a、b为常数).
(1)求函数 在点(1,
在点(1, )处的切线方程;
)处的切线方程;
(2)当函数g(x)在x=2处取得极值-2.求函数 的解析式;
的解析式;
(3)当 时,设
时,设 ,若函数
,若函数 在定义域上存在单调减区间,求实数b的取值范围;
在定义域上存在单调减区间,求实数b的取值范围;
(本题满分12分)已知函数f(x)=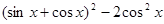 (
(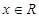 ).
).
(1)求函数f(x)的周期和递增区间;
(2)若函数 在[0,
在[0,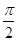 ]上有两个不同的零点x1、x2,求tan(x1+x2)的值.
]上有两个不同的零点x1、x2,求tan(x1+x2)的值.