如图,某小区拟在空地上建一个占地面积为2400平方米的矩形休闲广场,按照设计要求,休闲广场中间有两个完全相同的矩形绿化区域,周边及绿化区域之间是道路(图中阴影部分),道路的宽度均为2米.怎样设计矩形休闲广场的长和宽,才能使绿化区域的总面积最大?并求出其最大面积.
已知函数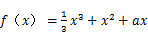 .
.
(1)若f(x)在区间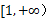 单调递增,求a的最小值;
单调递增,求a的最小值;
(2)若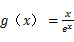 ,对
,对 ,使
,使 成立,求a的范围.
成立,求a的范围.
如图,在直三棱柱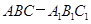 中,点D是
中,点D是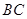 的中点.
的中点.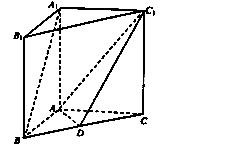
(1)求证: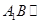 平面
平面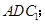
(2)若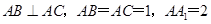 ,求平面
,求平面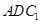 与
与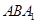 所成二面角的正弦值.
所成二面角的正弦值.
某大学外语系有5名大学生参加南京青奥会翻译志愿者服务,每名大学生都随机分配到奥体中心体操和游泳两个比赛项目(每名大学生只参加一个项目的服务).
(1)求5名大学生中恰有2名被分配到体操项目的概率;
(2)设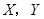 分别表示5名大学生分配到体操、游泳项目的人数,记
分别表示5名大学生分配到体操、游泳项目的人数,记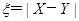 ,求随机变量
,求随机变量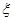 的分布列和数学期望
的分布列和数学期望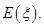
设数列 的前
的前 项和为
项和为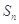 ,点
,点 在直线
在直线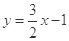 上.
上.
(1)求数列 的通项公式;
的通项公式;
(2)在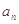 与
与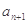 之间插入
之间插入 个数,使这
个数,使这 个数组成公差为
个数组成公差为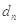 的等差数列,
的等差数列,
求数列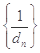 的前n项和
的前n项和 .
.
(本小题满分10分)选修4-5:不等式选讲
已知函数
(1)求函数 的值域
的值域
(2)求不等式: 的解集.
的解集.