(本小题满分13分)
已知椭圆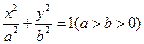 的左焦点为
的左焦点为 ,左右顶点分别为
,左右顶点分别为 ,上顶点为
,上顶点为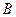 ,过
,过 三点作圆
三点作圆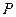 ,其中圆心
,其中圆心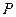 的坐标为
的坐标为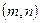 .
.
(Ⅰ)当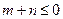 时,椭圆的离心率的取值范围.
时,椭圆的离心率的取值范围.
(Ⅱ)直线 能否和圆
能否和圆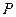 相切?证明你的结论.
相切?证明你的结论.
已知抛物线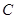 :
: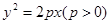 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.
(Ⅰ)求抛物线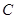 的方程;
的方程;
(Ⅱ)设直线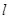 与抛物线
与抛物线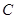 交于不同两点
交于不同两点 ,若满足
,若满足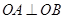 ,证明直线
,证明直线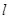 恒过定点,并求出定点
恒过定点,并求出定点 的坐标.
的坐标.
(Ⅲ)试把问题(Ⅱ)的结论推广到任意抛物线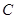 :
: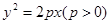 中,请写出结论,不用证明.
中,请写出结论,不用证明.
如图所示,平面 ⊥平面
⊥平面 ,
, ,
,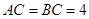 ,四边形
,四边形 是直角梯形,
是直角梯形,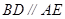 ,
,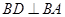 ,
, 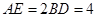 ,
, 分别为
分别为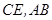 的中点.
的中点. 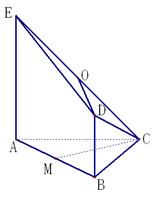
(Ⅰ) 用几何法证明: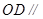 平面
平面 ;
;
(Ⅱ)用几何法证明: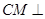 平面
平面 .
.
一个多面体的直观图与三视图如图所示, 分别是
分别是 中点
中点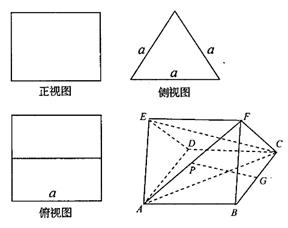
(Ⅰ)求此多面体的体积;
(Ⅱ)求证: .
.
已知椭圆 的左、右焦点分别是
的左、右焦点分别是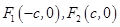 ,Q是椭圆外的动点,满足
,Q是椭圆外的动点,满足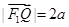 .点
.点 是线段
是线段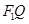 与该椭圆的交点,点T是
与该椭圆的交点,点T是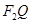 的中点.
的中点.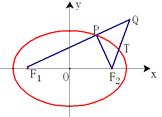
(Ⅰ)设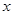 为点
为点 的横坐标,证明
的横坐标,证明 ;
;
(Ⅱ)求点T的轨迹 的方程.
的方程.
已知点 到两点
到两点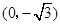 ,
, 的距离之和等于4,设点
的距离之和等于4,设点 的轨迹为
的轨迹为 ,直线
,直线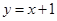 与轨迹
与轨迹 交于
交于 两点.
两点.
(Ⅰ)写出轨迹 的方程;
的方程;
(Ⅱ)求 的值.
的值.