已知甲盒内有大小相同的1个红球和
3个黑球，乙盒内有大小相同的1个红球和4个黑球
．现从甲、乙两个盒内各任取2个球．
（Ⅰ）求取出的4个球均为黑球的概率；
（II
）设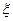
为取出的4个球中红球的个数，求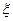的分布列和数学期望
已知函数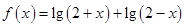
.
（1）求函数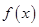
的定义域；
（2）若不等式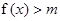
有解，求实数
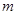的取值范围.
已知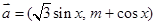
，
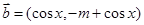, 且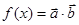
.
（1）求函数
的周期;
（2）当
时, 的最小值是－4 , 求此时函数的最大值, 及相应的
的值.
已知数列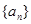
的前
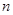项和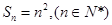
．
（1）求数列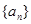的通项公式；
（2）若数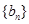
是等比数列，公比为
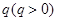且
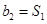
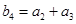,求数列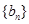的前n项和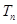
．
（本小题满分10分）选修4-5：不等式选讲
设函数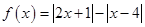
．
（1）解不等式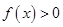
；
（2）若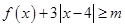
对一切实数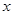
均成立，求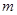
的取值范围．
（本小题满分10分）选修4-4：坐标系与参数方程
在直角坐标系中，以原点为极点，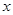
轴的正半轴为极轴建立坐标系．已知曲线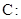
（
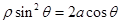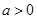），过点
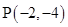的直线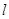
的参数方程为
（
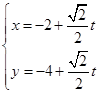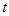是参数），直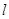线与曲线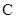
分别交于
、
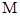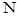两点．
（1）写出曲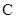线和直线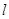的普通方程；
（2）若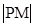
，
，
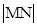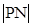成等比数列，求
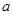的值．