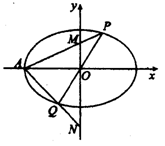
如图,在平面直角坐标系 中,离心率为
中,离心率为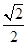 的椭圆
的椭圆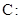
 (
(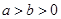 )的左顶点为
)的左顶点为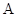 ,过原点
,过原点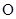 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆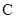 交于
交于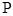 ,
,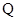 两点,直线
两点,直线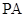 ,
,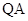 分别与
分别与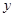 轴交于
轴交于 ,
,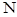 两点.当直线
两点.当直线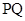 斜率为
斜率为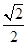 时,
时,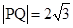 .
.
(1)求椭圆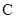 的标准方程;
的标准方程;
(2)试问以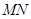 为直径的圆是否经过定点(与直线
为直径的圆是否经过定点(与直线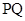 的斜率无关)?请证明你的结论.
的斜率无关)?请证明你的结论.
已知中心在原点的双曲线C的一个焦点是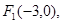 一条渐近线的方程是
一条渐近线的方程是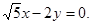
(Ⅰ)求双曲线C的方程;
(Ⅱ)若以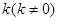 为斜率的直线
为斜率的直线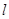 与双曲线C相交于两个不同的点M,N,且线段MN的垂直平分线与两坐标轴围成的三角形的面积为
与双曲线C相交于两个不同的点M,N,且线段MN的垂直平分线与两坐标轴围成的三角形的面积为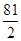 ,求
,求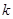 的取值范围.
的取值范围.
如图已知正四棱柱ABCD----A1B1C1D1,AB=1,AA1=2,点E为CC1的中点,点F为BD1的中点。
(1)证明:EF⊥平面 ;
;
(2)求点A1到平面BDE的距离;
(3)求BD1与平面BDE所成的角的余弦值.
若直线l: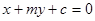 与抛物线
与抛物线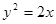 交于A、B两点,O点是坐标原点。
交于A、B两点,O点是坐标原点。
(1)当m=-1,c=-2时,求证:OA⊥OB;
(2)若OA⊥OB,求证:直线l恒过定点;并求出这个定点坐标。
(3)当OA⊥OB时,试问△OAB的外接圆与抛物线的准线位置关系如何?证明你的结论。
已知命题p:方程 表示焦点在y轴上的椭圆;命题q:双曲线
表示焦点在y轴上的椭圆;命题q:双曲线 的离心率
的离心率 ;若“
;若“ ”为真,“
”为真,“ ”为假,求实数
”为假,求实数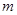 的取值范围.
的取值范围.
已知圆C:
(1)若不过原点的直线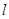 与圆C相切,且在
与圆C相切,且在 轴、
轴、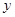 轴上的截距相等,求直线
轴上的截距相等,求直线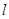 的方程;
的方程;
(2)从圆C外一点 向圆引一条切线,切点为M,O为坐标原点,且有
向圆引一条切线,切点为M,O为坐标原点,且有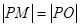 ,求点P的轨迹方程.
,求点P的轨迹方程.