如图已知正四棱柱ABCD----A1B1C1D1,AB=1,AA1=2,点E为CC1的中点,点F为BD1的中点。

(1)证明:EF⊥平面 ;
;
(2)求点A1到平面BDE的距离;
(3)求BD1与平面BDE所成的角的余弦值.
设函数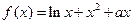 .
.
(Ⅰ)若x=时,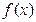 取得极值,求
取得极值,求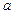 的值;
的值;
(Ⅱ)若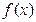 在其定义域内为增函数,求
在其定义域内为增函数,求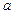 的取值范围;
的取值范围;
(Ⅲ)设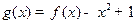 ,当
,当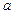 =-1时,证明
=-1时,证明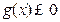 在其定义域内恒成立,并证明
在其定义域内恒成立,并证明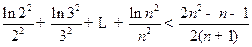 (
(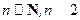 ).
).
设函数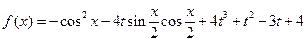 ,
,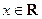 ,
,
其中|t|≤1,将f(x)的最小值记为g(t).
(1)求g(t)的表达式;
(2)对于区间[-1,1]中的某个t,是否存在实数a,使得不等式g(t)≤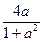 成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由.
成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由.
已知函数f(x)=x3+ax2+b的图象在点P(1,0)处的切线与直线3x+y=0平行,
(1)求常数a、b的值;
(2)求函数f(x)在区间[0,t]上的最小值和最大值。(t>0)
已知椭圆C: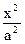 +
+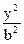 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为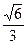 ,过右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点。
,过右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点。
(1)求直线ON(O为坐标原点)的斜率KON ;
(2)对于椭圆C上任意一点M,试证:总存在角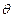 (
(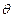 ∈R)使等式:
∈R)使等式: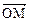 =cos
=cos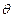
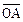 +sin
+sin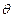
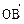 成立。
成立。
已知过点A(0,1),且方向向量为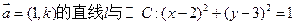 ,相交于M、N两点.
,相交于M、N两点.
(1)求实数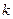 的取值范围;
的取值范围;
(2)求证: ;
;
(3)若O为坐标原点,且 .
.