（本小题满分12分）
三人独立破译同一份密码.已知三人各自破译出密码的概率分别为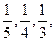
且他们是否破译出密码互不影响.
（Ⅰ）求恰有二人破译出密码的概率；
（Ⅱ）“密码被破译”与“密码未被破译”的概率哪个大？说明理由.
在
中，角A,B,C所对的边分别为a,b,c，且
（1）求角B的大小；
（2）若
，且
，求
的最小值．
已知二次函数
对任意
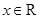，都有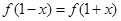
成立，设向量
（sinx，2），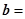
（2sinx，
），
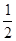（cos2x，1），
（1，2），当
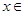[0，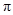
]时，求不等式f（
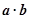）＞f（
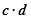）的解集．
已知圆
，
是直线
上的动点，
、
与圆
相切，切点分别为点
、
．
（1）若点的坐标为
，求切线、的方程；
（2）若点的坐标为
，求直线
的方程．
已知
，函数
．
（1）求
的对称轴方程；
（2）若对任意实数
，不等式
恒成立，求实数
的取值范围．
已知学生的数学成绩与物理成绩具有线性相关关系，某班6名学生的数学和物理成绩如表：
| 学生 学科 |
 |
 |
 |
 |
 |
 |
数学成绩（ ） |
83 |
78 |
73 |
68 |
63 |
73 |
物理成绩（ ） |
75 |
65 |
75 |
65 |
60 |
80 |
（1）求物理成绩对数学成绩的线性回归方程；
（2）当某位学生的数学成绩为70分时，预测他的物理成绩．
参考公式：用最小二乘法求线性回归方程
的系数公式：
参考数据：
，