(选修4-4:坐标系与参数方程) (本小题满分10分)
在直角坐标系xoy中,直线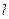 的参数方程为
的参数方程为 (t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为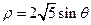 .
.
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设圆C与直线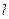 交于点A、B,若点P的坐标为
交于点A、B,若点P的坐标为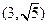 ,求|PA|+|PB|.
,求|PA|+|PB|.
.已知函数 的极大值点为
的极大值点为 .
.
(1)用实数 来表示实数
来表示实数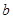 ,并求
,并求 的取值范围;
的取值范围;
(2)当 时,
时,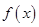 的最小值为
的最小值为 ,求
,求 的值;
的值;
(3)设 ,
, 两点的连线斜率为
两点的连线斜率为 .求证:必存在
.求证:必存在 ,使
,使 .
.
已知抛物线C: 过点
过点 。
。
(1)求抛物线的方程;
(2)是否存在平行于OA(O为原点)的直线L,与抛物线C有公共点,且直线OA与L的距离等于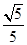 ?若存在,求直线L的方程;若不存在,说明理由。
?若存在,求直线L的方程;若不存在,说明理由。
已知函数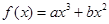 的图象经过点M(1,4),曲线在点M处的切线恰好与直线
的图象经过点M(1,4),曲线在点M处的切线恰好与直线 垂直,
垂直,
(1)求实数a、b的值;
(2)若函数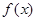 在区间[m,m+1]上单调递增,求m的取值范围.
在区间[m,m+1]上单调递增,求m的取值范围.
.已知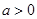 ,设p:函数
,设p:函数 在R上单调递减;命题q:方程
在R上单调递减;命题q:方程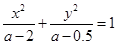 表示的曲线是双曲线,如果“p
表示的曲线是双曲线,如果“p q”为真,“p
q”为真,“p q”为假,求
q”为假,求 的取值范围.
的取值范围.
一个包装箱内有5件产品,其中3件正品,2件次品。现随机抽出两件产品,
(1)求恰好有一件次品的概率。
(2)求都是正品的概率。
(3)求抽到次品的概率。