小红今年12岁,她父亲比她大20岁,计算出她的父亲在几年后比她的年龄大一倍,那时他们2人的年龄各是多少?请你设计程序框图描述这一算法.
如图,
是直角梯形,
,
,
,
,又
,
,
,直线
与直线
所成的角为
.

(Ⅰ)求证:平面
平面
;
(Ⅱ)求二面角
的大小;
(Ⅲ)求三棱锥
的体积.
已知 , ,且 .
(Ⅰ)求
的值.
(Ⅱ)求
.
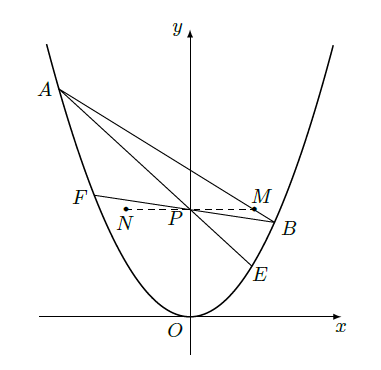
已知抛物线 和三个点 ,过点 的一条直线交抛物线于 、 两点, 、 的延长线分别交曲线 于 、 .
(1)证明
三点共线;
(2)如果
、
、
、
四点共线,问:是否存在
,使以线段
为直径的圆与抛物线有异于
、
的交点?如果存在,求出
的取值范围,并求出该交点到直线
的距离;若不存在,请说明理由.
已知函数
(1)求函数
的单调区间;
(2)若函数
的图像与直线
恰有两个交点,求
的取值范围.