(本小题满分16分)
函数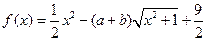 ,
,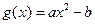 (
(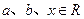 ),
),
A=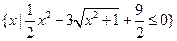
(Ⅰ)求集合A;
(Ⅱ)如果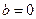 ,对任意
,对任意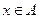 时,
时,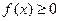 恒成立,求实数
恒成立,求实数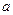 的范围;
的范围;
(Ⅲ)如果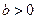 ,当“
,当“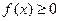 对任意
对任意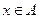 恒成立”与“
恒成立”与“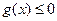 在
在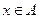 内必有解”同时成立时,求
内必有解”同时成立时,求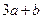 的最大值.
的最大值.
求下面各数列的前n项和:
(1) ,…
,…
(2) 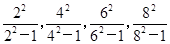 ,…
,…
已知an=
(1)求数列{an}的前10项和S10;
(2)求数列{an}的前2k项和S2k.
求下面数列的前n项和:
1 ,3
,3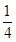 ,5
,5 ,7
,7 ,…
,…
已知数列{an}的首项a1=2a+1(a是常数,且a≠-1),
an=2an-1+n2-4n+2(n≥2),数列{bn}的首项b1=a,
bn=an+n2(n≥2).
(1)证明:{bn}从第2项起是以2为公比的等比数列;
(2)设Sn为数列{bn}的前n项和,且{Sn}是等比数列,求实数a的值;
(3)当a>0时,求数列{an}的最小项.
已知数列{an}的前n项和为Sn,a1=1,Sn+1=4an+1,设bn=an+1-2an.证明:数列{bn}是等比数列.