已知数列{an}的首项a1=2a+1(a是常数,且a≠-1),
an=2an-1+n2-4n+2(n≥2),数列{bn}的首项b1=a,
bn=an+n2(n≥2).
(1)证明:{bn}从第2项起是以2为公比的等比数列;
(2)设Sn为数列{bn}的前n项和,且{Sn}是等比数列,求实数a的值;
(3)当a>0时,求数列{an}的最小项.
如图1,在Rt△ABC中,∠C=90°,BC=6,AC=3,D,E分别是AC,AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
(1)求证: 平面
平面 ;
;
(2)过点E作截面
 平面
平面 ,分别交CB于F,
,分别交CB于F, 于H,求截面
于H,求截面 的面积。
的面积。
已知两直线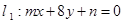 和
和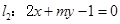 .试确定
.试确定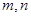 的值,使
的值,使
(1)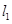 与
与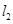 相交于点
相交于点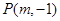 ;
;
(2)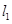 ∥
∥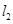 ;
;
(3)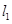
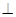
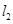 ,且
,且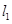 在
在 轴上的截距为-1.
轴上的截距为-1.
如图,空间四边形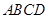 中,
中,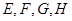 分别是
分别是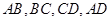 的中点,且
的中点,且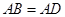 ,
,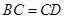 .
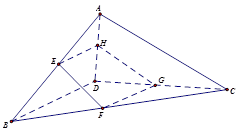
.
(1)求证: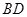
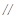 平面
平面 ;
;
(2)求证:四边形 是矩形.
是矩形.
已知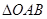 的顶点
的顶点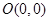 、
、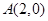 、
、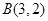 ,
,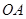 边上的中线所在直线为
边上的中线所在直线为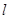 .
.
(Ⅰ)求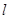 的方程;
的方程;
(Ⅱ)求点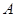 关于直线
关于直线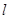 的对称点的坐标.
的对称点的坐标.
设函数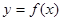 是定义在
是定义在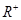 上的减函数,并且满足
上的减函数,并且满足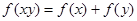 ,且
,且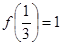 .
.
(1)求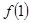 的值;
的值;
(2)如果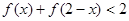 ,求
,求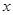 的取值范围.
的取值范围.