已知数列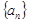 满足
满足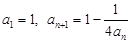 ,其中
,其中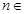 N*.
N*.
(Ⅰ)设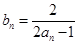 ,求证:数列
,求证:数列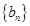 是等差数列,并求出
是等差数列,并求出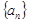 的通项公式
的通项公式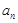 ;
;
(Ⅱ)设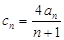 ,数列
,数列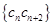 的前
的前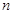 项和为
项和为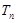 ,是否存在正整数
,是否存在正整数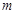 ,使得
,使得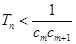 对于
对于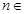 N*恒成立,若存在,求出
N*恒成立,若存在,求出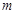 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
已知甲箱中只放有x个红球与y个白球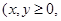 且
且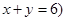 ,乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外,无其它区别). 若甲箱从中任取2个球, 从乙箱中任取1个球.
,乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外,无其它区别). 若甲箱从中任取2个球, 从乙箱中任取1个球.
(Ⅰ)记取出的3个球的颜色全不相同的概率为P,求当P取得最大值时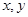 的值;
的值;
(Ⅱ)当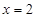 时,求取出的3个球中红球个数
时,求取出的3个球中红球个数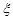 的期望
的期望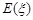 .
.
设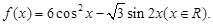 .
.
(Ⅰ)求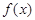 的最大值及最小正周期;
的最大值及最小正周期;
(Ⅱ)在△ABC中,角A,B,C的对边分别为a,b,c,锐角A满足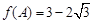 ,
,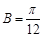 ,求
,求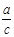 的值.
的值.
已知函数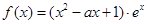 .
.
(1)当 时,求曲线
时,求曲线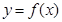 在点
在点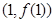 处的切线方程;
处的切线方程;
(2)对任意 ,
, 在区间
在区间 上是增函数,求实数
上是增函数,求实数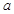 的取值范围.
的取值范围.
如图,在四棱锥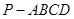 中,底面
中,底面 是矩形,
是矩形, 分别为
分别为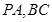 的中点,
的中点, ,且
,且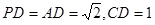

(1)证明: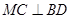 ;
;
(2)求二面角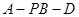 的余弦值。
的余弦值。