已知甲箱中只放有x个红球与y个白球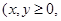 且
且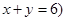 ,乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外,无其它区别). 若甲箱从中任取2个球, 从乙箱中任取1个球.
,乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外,无其它区别). 若甲箱从中任取2个球, 从乙箱中任取1个球.
(Ⅰ)记取出的3个球的颜色全不相同的概率为P,求当P取得最大值时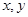 的值;
的值;
(Ⅱ)当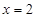 时,求取出的3个球中红球个数
时,求取出的3个球中红球个数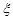 的期望
的期望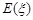 .
.
若随机事件A在1次试验中发生的概率是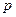 ,用随机变量
,用随机变量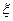 表示A在1次实验中发生的次数。(1)求方差
表示A在1次实验中发生的次数。(1)求方差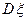 的最大值;(2)求
的最大值;(2)求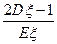 的最大值。
的最大值。
高二(十)班共50名同学,其中35名男生,15名女生,随机从中取出5名同学参加学生代表大会,所取出的5名学生代表中,女生人数X的频率分布如何?
设 100 件产品中有 70 件一等品,25 件二等品,规定一、二等品为合格品.从中任取1 件,求 (1) 取得一等品的概率;(2) 已知取得的是合格品,求它是一等品的概率.
甲乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为
,乙队中3人答对的概率分别为
且各人正确与否相互之间没有影响.用
表示甲队的总得分.
(Ⅰ)求随机变量
分布列;
(Ⅱ)用
表示"甲、乙两个队总得分之和等于3"这一事件,用B表示"甲队总得分大于乙队总得分"这一事件,求
.
一张储蓄卡的密码共有6位数,每位数字都可从0~9中任选,某人在银行自动提款机上取钱时,忘记了密码的最后一位数字,求:
⑴按第一次不对的情况下,第二次按对的概率;
⑵任意按最后一位数字,按两次恰好按对的概率;
⑶若他记得密码的最后一位是偶数,不超过2次就按对的概率