在直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为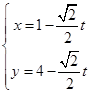 (t为参数),再以原点为极点,以x正半轴为极轴建立坐标系,并使得它与直角坐标系有相同的长度单位,在该极坐标系中圆C的方程为
(t为参数),再以原点为极点,以x正半轴为极轴建立坐标系,并使得它与直角坐标系有相同的长度单位,在该极坐标系中圆C的方程为 .
.
(1)求圆C的直角坐标方程;
(2)设圆C与直线 将于点
将于点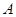 、
、 ,若点
,若点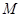 的坐标为
的坐标为 ,求
,求 的值.
的值.
((12分)大学毕业生小明到甲、乙、丙三个单位应聘,其被录用的概率分别为 (各单位是否录用他相互独立,允许小明被多个单位同时录用)(1)求小明没有被录用的概率;(2)设录用小明的单位个数为
(各单位是否录用他相互独立,允许小明被多个单位同时录用)(1)求小明没有被录用的概率;(2)设录用小明的单位个数为 ,求
,求 的分布列和它的数学期望。
的分布列和它的数学期望。
()已知函数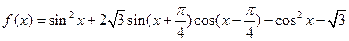 .
.
(1)求函数 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(已知二次函数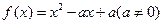 ,不等式
,不等式 的解集有且只有一个元素,设数列
的解集有且只有一个元素,设数列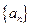 的前
的前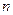 项和为
项和为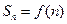 .(1)求数列
.(1)求数列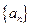 的通项公式;(2)设各项均不为
的通项公式;(2)设各项均不为 的数列
的数列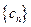 中,满足
中,满足 的正整数
的正整数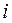 的个数称作数列
的个数称作数列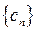 的变号数,令
的变号数,令 ,求数列
,求数列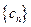 的变号数.
的变号数.
已知函数 ,其中 .
(Ⅰ)当 时,讨论函数 的单调性;
(Ⅱ)若函数 仅在 处有极值,求 的取值范围;
(Ⅲ)若对于任意的 ,不等式 在 上恒成立,求 的取值范围.
(本小题满分14分)已知二次函数 .(1)若
.(1)若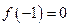 ,试判断函数
,试判断函数 零点个数;(2)若对
零点个数;(2)若对 且
且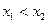 ,
, ,试证明
,试证明 ,使
,使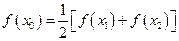 成立。(3)是否存在
成立。(3)是否存在 ,使
,使 同时满足以下条件①对
同时满足以下条件①对 ,且
,且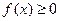 ;②对
;②对 ,都有
,都有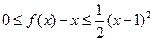 。若存在,求出
。若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。