袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为 ,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用
,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用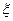 表示取球终止所需要的取球次数.
表示取球终止所需要的取球次数.
(1)求袋中原有白球的个数;
(2)求随机变量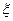 的概率分布;
的概率分布;
(3)求甲取到白球的概率.
(本小题满分12分)已知:函数 对一切实数
对一切实数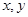 都有
都有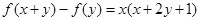 成立,且
成立,且 .
.
(1)求 的值;
的值;
(2)求 的解析式;
的解析式;
(3)已知 ,设
,设 :当
:当 时,不等式
时,不等式 恒成立;
恒成立; :当
:当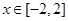 时,
时,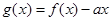 是单调函数.如果满足
是单调函数.如果满足 成立的
成立的 的集合记为
的集合记为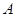 ,满足
,满足 成立的
成立的 的集合记为
的集合记为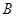 ,求
,求 (
( 为全集).
为全集).
(本小题满分12分)某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.
为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)求在这10个卖场中,甲型号电视机的“星级卖场”的个数;
(2)若在这10个卖场中,乙型号电视机销售量的平均数为26.7,求 的概率;
的概率;
(3)若a=1,记乙型号电视机销售量的方差为 ,根据茎叶图推断b为何值时,
,根据茎叶图推断b为何值时, 达到最小值.(只需写出结论)
达到最小值.(只需写出结论)
(本小题满分12分)数列{ }的前
}的前 项和为
项和为 ,
, 是
是 和
和 的等差中项,等差数列{
的等差中项,等差数列{ }满足
}满足 ,
, .
.
(1)求数列 ,
,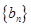 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列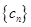 的前
的前 项和
项和 .
.
(本小题满分12分)在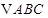 中,角
中,角 的对边分别为
的对边分别为 ,且满足
,且满足
(1)求角 的大小;
的大小;
(2)若 ,求
,求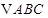 面积的最大值。
面积的最大值。
(本小题满分12分)已知函数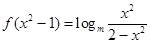
(1)求 的解析式并判断
的解析式并判断 的奇偶性;
的奇偶性;
(2)解关于 的不等式
的不等式