(本小题满分14分)
已知数列{an}中,a1="1" ,a2=3,且点(n,an)满足函数y = kx + b.
(1)求k,b的值,并写出数列{an}的通项公式;
(2)记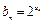 ,求数列{bn}的前n和Sn.
,求数列{bn}的前n和Sn.
(本小题满分14分)已知函数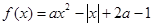 (a为实常数)。
(a为实常数)。
(1)若a=1,求 的单调区间;
的单调区间;
(2)若 ,设
,设 在区间
在区间 的最小值为
的最小值为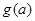 ,求
,求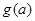 的表达式;
的表达式;
(3)设 ,若函数
,若函数 在区间
在区间 上是增函数,求实数a的取值范围。
上是增函数,求实数a的取值范围。
(本小题满分13分)已知商品的价格上涨 ,销售的数量就减少
,销售的数量就减少 ,其中m为正常数。
,其中m为正常数。
(1)当 时,该商品的价格上涨多少,就能使销售的总金额最大?
时,该商品的价格上涨多少,就能使销售的总金额最大?
(2)如果适当地涨价,能使销售金额增加,求m的取值范围。
(本小题满分12分)已知偶函数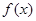 ,对任意
,对任意 ,恒有
,恒有 。求:
。求:
(1) ,
,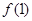 ,
,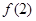 的值;
的值;
(2)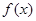 的表达式;
的表达式;
(3) 在
在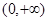 上的最值。
上的最值。
(本小题满分12分)设当 时,
时,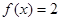 。当
。当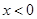 时,
时, ,又
,又 ,写出
,写出 的表达式并作出其图象。
的表达式并作出其图象。
(本小题满分12分)已知函数 是幂函数,且当
是幂函数,且当 时为减函数,
时为减函数,
(1)求实数m的值;
(2)判断函数 奇偶性并说明理由。
奇偶性并说明理由。