在平面直角坐标系上,设不等式组 所表示的平面区域为
所表示的平面区域为 ,记
,记 内的整点(即横坐标和纵坐标均为整数的点)的个数为
内的整点(即横坐标和纵坐标均为整数的点)的个数为
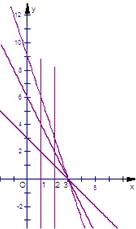
(1)求 ;并求数列
;并求数列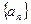 的通项公式
的通项公式 ;
;
(2)数列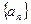 的和前
的和前 项为
项为 ,求数列
,求数列 的前n项和;
的前n项和;
(3)设 ,数列
,数列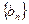 的和前
的和前 项为
项为 ,求证:
,求证: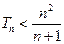
设函数f(x)=sin( x-
x- )-2cos2
)-2cos2 x+1(1)求f(x)的最小正周期(2)若函数y=g(x)与f(x)的图象关于直线x=1对称,求当x∈[0,
x+1(1)求f(x)的最小正周期(2)若函数y=g(x)与f(x)的图象关于直线x=1对称,求当x∈[0, ]时,y=g(x)的最大值
]时,y=g(x)的最大值
(本小题满分14分)数列 中,
中, ,
, 为其前
为其前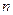 项的和,满足
项的和,满足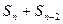 =
=
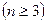 ,令
,令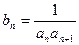 (Ⅰ)求数列
(Ⅰ)求数列 的通项公式(Ⅱ)若
的通项公式(Ⅱ)若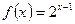 ,求证:
,求证: (Ⅲ)设
(Ⅲ)设 ,求证数列
,求证数列
(本小题满分12分)已知函数 ,
,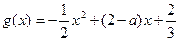
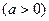 (Ⅰ)求f (x)的单调递增区间;(Ⅱ)若在区间[0,
(Ⅰ)求f (x)的单调递增区间;(Ⅱ)若在区间[0,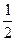 ]内至少存在一实数
]内至少存在一实数 x0使得
x0使得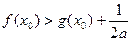 成立,求实数a的取值范围.
成立,求实数a的取值范围.
(本小题满分12分)设函数
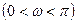 ,将
,将 的图象按
的图象按 平移后得一奇函数 (Ⅰ)求当
平移后得一奇函数 (Ⅰ)求当 时函数
时函数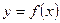 的值域(Ⅱ)设数列
的值域(Ⅱ)设数列 的通项公式为
的通项公式为
 ,
, 为其前
为其前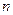 项的和, 求
项的和, 求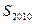 的值
的值
(本小题满分12分)递增等比数列{an}中a1=2,前n项和为Sn,S2是a2,a3的等差中项:(Ⅰ)求Sn及an;(Ⅱ)数列{bn}满足 的前n项和为Tn,求
的前n项和为Tn,求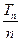 的最小值.
的最小值.