(选修模块3—3)
（1）下列叙述正确的是（ ▲ ）
A．一定质量的气体压强越大，则分子的平均动能越大
B．当分子间距离变大时，分子间引力和斥力都减小
C．外界对气体做正功，气体的内能一定增加
D．从分子动理论观点来看，决定物体温度的因素是分子势能
（2）关于热现象和热学规律，下列说法中正确的是 （ ▲ ）
A．只要知道气体的摩尔体积和阿伏加德罗常数，就可以算出气体分子的体积
B．悬浮在液体中的固体颗粒越小，布朗运动就越明显
C．第一类永动机它违反能量守恒定律故不可能制成
D．容器内气体的压强是由容器中气体的重力作用引起的
（3）如图所示，是一定质量的理想气体状态变化的过程中密度ρ随热力学温度T变化的图线，由图线可判断A→B过程中气体的压强 ▲ （填“增大”“不变”或“减小”）， B到C过程气体压强 ▲ (填“增大”“不变”或“减小”)，B→C过程中 ▲ （填“气体膨胀对外做功”“气体不做功”或“外界对气体做功”）。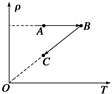
（4）我国陆地面积S = 9.6×1012 m2，若地面大气压 P0 = 1.0×105Pa，地面附近重力加速度g = 10m/s2，空气平均犘尔质量为M0 = 3.0×10-2kg.mol-1，附伏伽德罗常数NA = 6.0×1023 mol-1。
①我国陆地上空空气总质量大约为多少？
②我国陆地上空空气总分子数大约为多少？
如图所示，两根足够长的光滑平行金属导轨相距为L，导轨平面与水平面成θ角，上端通过导线连接阻值为R的电阻，阻值为r的金属棒ab放在两导轨上，棒与导轨垂直并保持良好接触，整个装置处在垂直导轨平面向上的磁场中，若所加磁场的磁感应强度大小恒为B，使金属棒沿导轨由静止向下运动，当t=t0时刻，物体下滑距离为s，此时金属棒恰好以速度v0匀速运动。已知重力加速度为g。试求：
（1）求导体棒质量m的大小；
（2）在t0时间内产生的总热量Q．
如图所示，在x轴上方有垂直于xy平面向里的匀强磁场，磁感应强度为B；在x轴下方有沿y轴负方向的匀强电场，场强为E。一质量为m，电荷量为-q的粒子从坐标原点O沿着y轴正方向射出。射出之后，第三次到达x轴时，它与点O的距离为L。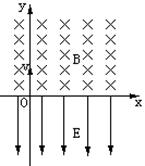
（1）求此粒子射出时的速度v
（2）运动的总路程s（重力不计）。
如图，线圈abcd的面积是0.05 m2，共100匝，线圈电阻为1 Ω，外接电阻R为9 Ω，匀强磁场的磁感应强度为B＝
T，当线圈以300 r/min的转速匀速旋转时，求： 
(1)若从线圈处于中性面开始计时，写出线圈中感应电动势的瞬时值表达式；
(2)电路中，电压表和电流表的示数各是多少？
(10分). “┙”型滑板，（平面部分足够长），质量为4m，距滑板的A壁为L1距离的B处放有一质量为m，电量为+q的大小不计的小物体，小物体与板面的摩擦不计，整个装置处于场强为E的匀强电场中，初始时刻，滑板与小物体都静止，试求：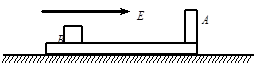
(1)释放小物体，第一次与滑板A壁碰前小物体的速度v1多大？
(2)若小物体与A壁碰后相对水平面的速度大小为碰前的
，碰撞时间极短，则碰撞后滑板速度多大？（均指对地速度）
(3)若滑板足够长，小物体从开始运动到第二次碰撞前，电场力做功为多大？
(8分).如图，一绝缘细圆环半径为r，环面处于水平面内，场强为E的匀强电场与圆环平面平行.环上穿有一电量为+q、质量为m的小球，可沿圆环做无摩擦的圆周运动.若小球经A点时速度的方向恰与电场垂直，且圆环与小球间沿水平方向无力的作用(设地球表面重力加速度为g).则：
(1)小球经过A点时的速度大小vA是多大？
(2)当小球运动到与A点对称的B点时，小球的速度是多大？圆环对小球的作用力大小是多少？
(3)若Eq=mg，小球的最大动能为多少？