如图所示,滑块的质量M=2kg,开始静止在水平面上的A点,滑块与水平面间的摩擦因数为 ,与A点相距s=2.25m的B点上方有一质量m=1.2kg的小球,小球被一长为
,与A点相距s=2.25m的B点上方有一质量m=1.2kg的小球,小球被一长为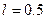 米的轻绳紧挂在O点而处于静止状态。现给滑块一瞬时冲量I=10N·s,让滑块沿水平面向右运动,此后与小球发生碰撞,碰后小球恰能在竖直平面内完成完整的圆周运动(g取10m/s2)。求:滑块最终静止在距离A点多远处?因滑块与小球碰撞而损失的机械能是多少?
米的轻绳紧挂在O点而处于静止状态。现给滑块一瞬时冲量I=10N·s,让滑块沿水平面向右运动,此后与小球发生碰撞,碰后小球恰能在竖直平面内完成完整的圆周运动(g取10m/s2)。求:滑块最终静止在距离A点多远处?因滑块与小球碰撞而损失的机械能是多少?
如图所示,一定质量的理想气体从状态A经等压过程到状态B。此过程中,气体压强p=1.0×105Pa,吸收的热量Q=7.0×102J, 求此过程中气体内能的增量。
半径为R,均匀带正电荷的球体在空间产生球对称的电场;场强大小沿半径分布如图所示,图中E0已知,E-r曲线下O-R部分的面积等于R-2R部分的面积。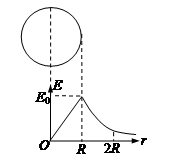
(1)写出E-r曲线下面积的单位;
(2)己知带电球在r≥R处的场强E=kQ/r2,式中k为静电力常量,该均匀带电球所带的电荷量Q为多大?
(3)求球心与球表面间的电势差ΔU;
(4)质量为m,电荷量为q的负电荷在球面处需具有多大的速度可以刚好运动到2R处?
如图所示,两块相同的金属板正对着水平放置,板间距离为 d 。当两板间加电压 U 时,一个质量为m、电荷量为 + q的带电粒子,以水平速度 v0 从A点射入电场,经过一段时间后从B点射出电场,A、B间的水平距离为 L ,不计重力影响。求:
(1)带电粒子从A点运动到B点经历的时间;
(2)带电粒子经过B点时速度的大小;
(3)A、B间的电势差。
图中E=10V,R1=4Ω,R2=6Ω,C=30μF。(电源内阻不计)[
(1)闭合电键K,求稳定后通过R1的电流
(2)然后将电键K断开,求这以后流过R1的总电量
(13分)如图所示,一足够长的水平传送带以速度v0匀速运动,质量均为m的小物块P和小物块Q由通过滑轮组的轻绳连接,轻绳足够长且不可伸长.某时刻物块P从传送带左端以速度2v0冲上传送带,P与定滑轮间的绳子水平.已知物块P与传送带间的动摩擦因数μ=0.25,重力加速度为g,不计滑轮的质量与摩擦.求: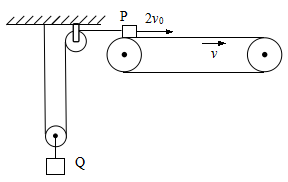
(1)运动过程中小物块P、Q的加速度大小之比;
(2)物块P刚冲上传送带到右方最远处的过程中,PQ系统机械能的改变量;
(3)若传送带以不同的速度v(0<v<2v0)匀速运动,当v取多大时物块P向右冲到最远处时,P与传送带间产生的摩擦热最小?最小值为多大?