已知数列 的前
的前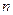 和为
和为 ,且满足
,且满足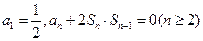 。
。
(1)问:数列 是否为等差数列?并证明你的结论;
是否为等差数列?并证明你的结论;
(2)求 ;
;
(3)求证: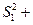


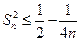 。
。
(本小题满分14分)已知函数 。
。 (I)当
(I)当 时,函数
时,函数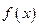 取得极大值,求实数
取得极大值,求实数 的值;
的值;
(II)若存在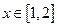 ,使不等式
,使不等式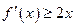 成立,其中
成立,其中 为
为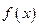 的导函数,求实数
的导函数,求实数 的取值范围;
的取值范围;
(III)求函数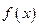 的单调区间。
的单调区间。
已知椭圆的中心在原点,焦点在x 轴上,离心率为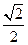 ,且椭圆经过圆C:
,且椭圆经过圆C: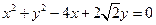 的圆心C。
的圆心C。
(1)求椭圆的方程;
(2)设直线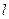 过椭圆的焦点且与圆C相切,求直线
过椭圆的焦点且与圆C相切,求直线 的方程。
的方程。
如图,在梯形ABCD中,AB∥CD,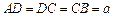 ,
,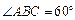 ,平面
,平面 平面
平面 ,四边形
,四边形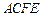 是矩形,
是矩形,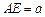 ,点
,点 在线段
在线段 上。
上。
(1)求证: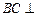 平面
平面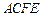 ;
;
(2)当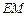 为何值时,
为何值时,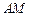 ∥平面
∥平面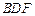 ?写出结论,并加以证明;
?写出结论,并加以证明;
(3)当EM为何值时,AM⊥BE?写出结论,并加以证明。
求与向量 =
=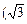 ,-1)和
,-1)和 =(1,
=(1, )夹角相等,且模为
)夹角相等,且模为 的向量
的向量 的坐标。
的坐标。
已知△ABC中,A(2,-1),B(3,2),C(-3,-1),BC边上的高为AD,求点D和向量 坐标。
坐标。