求证:方程x2+ax+1=0的两实根的平方和大于3的必要条件是|a|> ,这个条件是其充分条件吗?为什么?
,这个条件是其充分条件吗?为什么?
已知函数f(x)在区间(-∞,+∞)上是增函数,a,b∈R.
(1)求证:若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b);
(2)判断(1)中命题的逆命题是否正确,并证明你的结论.
已知二次函数f(x)=ax2+x,若对任意x1,x2∈R,恒有2f(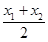 )≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.
)≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.
(1)求集合A;
(2)设集合B={x||x+4|<a},若集合B是集合A的子集,求a的取值范围.
已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1}.
(1)若A∪B=A,求实数m的取值范围;
(2)当x∈Z时,求A的非空真子集的个数;
(3)当x∈R时,若A∩B=∅,求实数m的取值范围.
已知集合A={x| ≥1,x∈R},B={x|x2-2x-m<0}.
≥1,x∈R},B={x|x2-2x-m<0}.
(1)当m=3时,求A∩(∁RB);
(2)若A∩B={x|-1<x<4},求实数m的值.