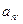已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)求函数 在区间
在区间 上的最大值.(其中
上的最大值.(其中 是自然对数的底数)
是自然对数的底数)
(本小题满分13分)已知函数 ,数列
,数列 满足
满足
(1)若数列 是常数列,求t的值;
是常数列,求t的值;
(2)当 时,记
时,记 ,证明:数列
,证明:数列 是等比数列,并求出通项公式an.
是等比数列,并求出通项公式an.
(本小题满分13分)已知
(1)求 的最大值,及当取最大值时x的取值集合。
的最大值,及当取最大值时x的取值集合。
(2)在三角形ABC中,a,b,c分别是角A,B,C所对的边,对定义域内任意x,有 的最大值.
的最大值.
(本小题满分12分)如图,在多面体ABCDE中,AE⊥面ABC,DB//AE,且AC=AB=BC=AE=1,BD=2,F为CD中点。
(1)求证:EF⊥平面BCD;
(2)求多面体ABCDE的体积;
(3)求平面ECD和平面ACB所成的锐二面角的余弦值。
(本小题满分12分)一个盒子中装有5张卡片,每张卡片上写有一个数字,数字分别是1、2、3、4、5,现从盒子中随机抽取卡片。
(1)从盒中依次抽取两次卡片,每次抽取一张,取出的卡片不放回,求两次取到的卡片的数字既不全是奇数,也不全是偶数的概率;
(2)若从盒子中有放回的抽取3次卡片,每次抽取一张,求恰有两次取到卡片的数字为偶数的概率;
(3)从盒子中依次抽取卡片,每次抽取一张,取出的卡片不放回,当放回记有奇数的卡片即停止抽取,否则继续抽取卡片,求抽取次数X的分布列和期望。
(本小题满分13分)
已知数列 的前n项和
的前n项和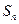 与通项
与通项 之间满足关系
之间满足关系
(I)求数列 的通项公式;
的通项公式;
(II)设 求
求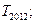
(III)若 ,求
,求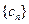 的前n项和
的前n项和