已知以函数
的图象上的点
为切点的切线的倾斜角为
．
（1）求
的值；
（2）是否存在正整数
，使不等式
对于
恒成立？若存在，求出最小的正整数，若不存在，说明理由；
（3）对于
，比较
与
的大小．
（本小题满分14分）
如图所示的多面体，它的正视图为直角三角形，侧视图为正三角形，俯视图为正方形（尺寸如图所示），E为VB的中点．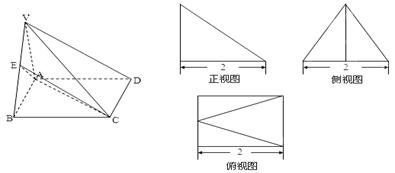
(1)求证：VD∥平面EAC；
(2)求二面角A—VB—D的余弦值．
(本小题满分14分)（1）一个圆与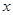
轴相切，圆心在直线
上，且被直线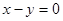
所截得的弦长为
，求此圆方程。
（2）已知圆
，直线
，求与圆
相切，且与直线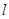
垂直的直线方程。
(本小题满分14分)
在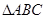
中，角
的对边分别为
，
，
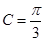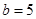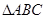，的面积为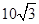
．
（Ⅰ）求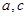
的值；
（Ⅱ）求
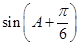的值．
(本题满分14分) 已知
是方程
的两个不等实根，函数
的定义域为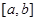
．
⑴当
时，求函数
的值域；
⑵证明：函数在其定义域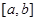上是增函数；
⑶在（1）的条件下，设函数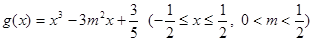
，
若对任意的
，总存在
，使得
成立，
求实数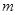
的取值范围．
（本小题满分15分） 已知动圆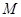
过定点
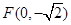，且与直线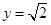
相切，椭圆
的对称轴为坐标轴，一个焦点是
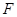，点
在椭圆上．
（Ⅰ）求动圆圆心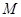的轨迹
的方程及其椭圆的方程；
（Ⅱ）若动直线
与轨迹在
处的切线平行，且直线与椭圆交于
两点，问：是否存在着这样的直线使得
的面积等于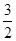
？如果存在，请求出直线的方程；如果不存在，请说明理由．