(本小题满分14分)
在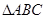 中,角
中,角 的对边分别为
的对边分别为 ,
,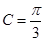 ,
,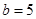 ,
,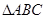 的面积为
的面积为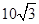 .
.
(Ⅰ)求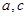 的值;
的值;
(Ⅱ)求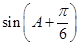 的值.
的值.
已知O为坐标原点,点A、B的坐标分别为A(a,0)、B(0,a),其中常数a>0,点P在线段AB上,且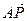 =λ
=λ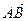 (0≤λ≤1),求
(0≤λ≤1),求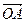 ·
·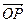 的最大值.
的最大值.
若f(x)=2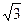 sin
sin cos
cos -2sin2
-2sin2 .(1)若x∈[0,π],求f(x)的值域;(2)在△ABC中,A、B、C所对边分别为a、b、c,若f(C)=1,且b2=ac,求sinA的值.
.(1)若x∈[0,π],求f(x)的值域;(2)在△ABC中,A、B、C所对边分别为a、b、c,若f(C)=1,且b2=ac,求sinA的值.
已知函数f(x)=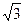 sin
sin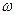 xcos
xcos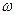 x-cos2
x-cos2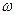 x,其中
x,其中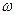 为使函数f(x)能在x=
为使函数f(x)能在x= 时取得最大值时的最小正整数.
时取得最大值时的最小正整数.
(1)求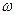 的值;
的值;
(2)设△ABC的三边 a、b、c满足b2=ac,且边b所对的角
a、b、c满足b2=ac,且边b所对的角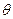 的取值集合为A,当x
的取值集合为A,当x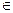 A时,求函数f(x)的值域.
A时,求函数f(x)的值域.
已知函数
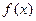 =
=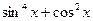 ,若
,若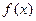 =
=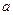 有解,求实数
有解,求实数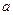 的取值范围.
的取值范围.
已知向量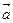 =(cos
=(cos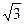 x,sin
x,sin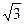 x),
x),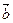 =(cos
=(cos ,sin
,sin )(0
)(0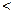

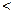
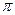 ).
).
设函数f(x)=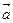 ·
·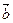 ,且f(x)+
,且f(x)+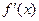 为偶函数.(1)求
为偶函数.(1)求 的值;
的值;
(2)求f(x)的单调增区间.